algorithm strategies of problem solving

EnjoyMathematics

Problem-Solving Approaches in Data Structures and Algorithms

This blog highlights some popular problem-solving strategies for solving problems in DSA. Learning to apply these strategies could be one of the best milestones for the learners in mastering data structure and algorithms.

An Incremental approach using Single and Nested loops

One of the simple ideas of our daily problem-solving activities is that we build the partial solution step by step using a loop. There is a different variation to it:

• Input-centric strategy: At each iteration step, we process one input and build the partial solution.
• Output-centric strategy: At each iteration step, we add one output to the solution and build the partial solution.
• Iterative improvement strategy: Here, we start with some easily available approximations of a solution and continuously improve upon it to reach the final solution.

Here are some approaches based on loop: Using a single loop and variables, Using nested loops and variables, Incrementing the loop by a constant (more than 1), Using the loop twice (Double traversal), Using a single loop and prefix array (or extra memory), etc.

Example problems:   Insertion Sort ,  Finding max and min in an array ,  Valid mountain array ,  Find equilibrium index of an array ,  Dutch national flag problem ,  Sort an array in a waveform .

Decrease and Conquer Approach

This strategy is based on finding the solution to a given problem via its one sub-problem solution. Such an approach leads naturally to a recursive algorithm, which reduces the problem to a sequence of smaller input sizes. Until it becomes small enough to be solved, i.e., it reaches the recursion’s base case.

Example problems:   Euclid algorithm of finding GCD ,  Binary Search ,  Josephus problem

Problem-solving using Binary Search

When an array has some order property similar to the sorted array, we can use the binary search idea to solve several searching problems efficiently in O(logn) time complexity. For doing this, we need to modify the standard binary search algorithm based on the conditions given in the problem. The core idea is simple: calculate the mid-index and iterate over the left or right half of the array.

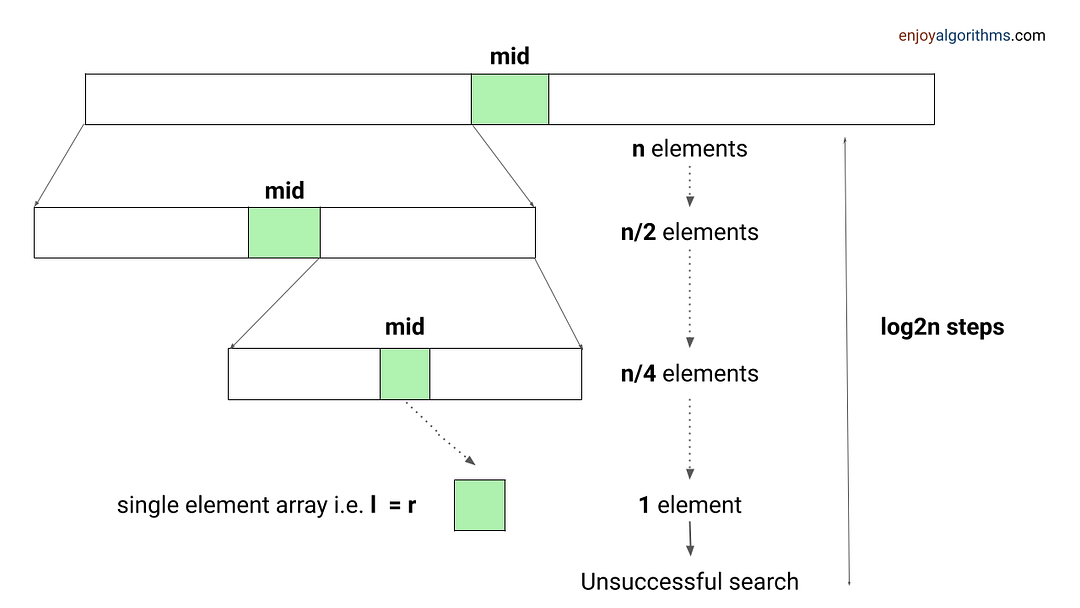
Example problems: Find Peak Element , Search a sorted 2D matrix , Find the square root of an integer , Search in Rotated Sorted Array

Divide and Conquer Approach

This strategy is about dividing a problem into  more than one subproblems,  solving each of them, and then, if necessary, combining their solutions to get a solution to the original problem. We solve many fundamental problems efficiently in computer science by using this strategy.

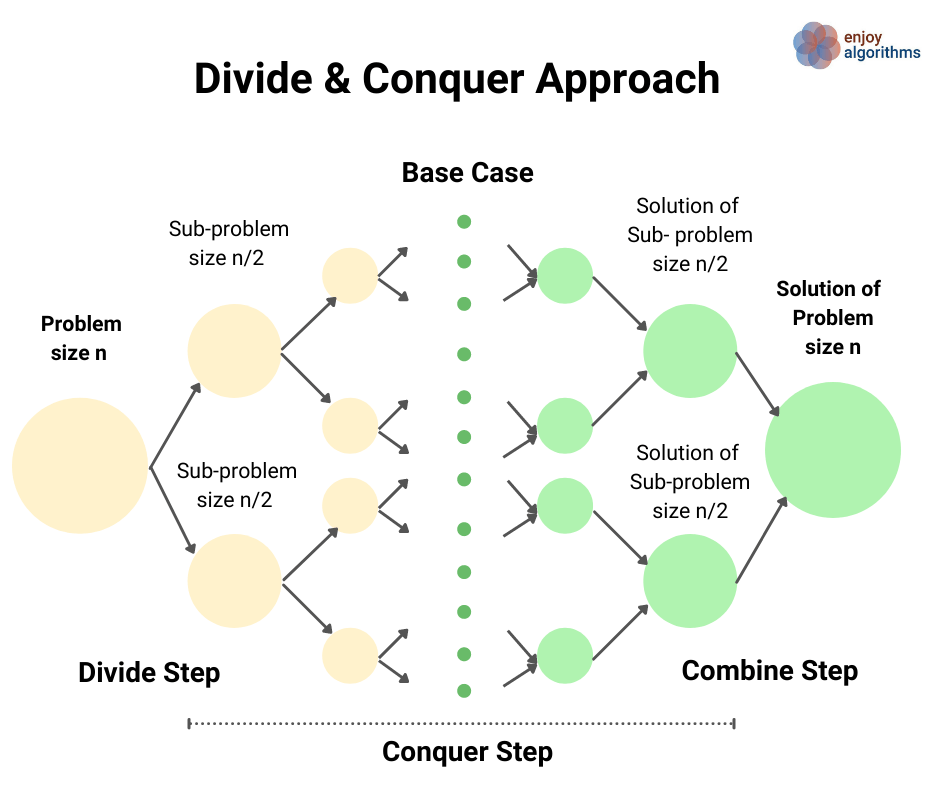
Example problems:   Merge Sort ,  Quick Sort ,  Median of two sorted arrays

Two Pointers Approach

The two-pointer approach helps us optimize time and space complexity in the case of many searching problems on arrays and linked lists. Here pointers can be pairs of array indices or pointer references to an object. This approach aims to simultaneously iterate over two different input parts to perform fewer operations. There are three variations of this approach:

Pointers are moving in the same direction with the same pace:   Merging two sorted arrays or linked lists, Finding the intersection of two arrays or linked lists , Checking an array is a subset of another array , etc.

Pointers are moving in the same direction at a different pace (Fast and slow pointers):   Partition process in the quick sort , Remove duplicates from the sorted array , Find the middle node in a linked list , Detect loop in a linked list , Move all zeroes to the end , Remove nth node from list end , etc.

Pointers are moving in the opposite direction:  Reversing an array, Check pair sum in an array , Finding triplet with zero-sum , Rainwater trapping problem , Container with most water , etc.

Sliding Window Approach

A sliding window concept is commonly used in solving array/string problems. Here, the window is a contiguous sequence of elements defined by the start and ends indices. We perform some operations on elements within the window and “slide” it in a forward direction by incrementing the left or right end.

This approach can be effective whenever the problem consists of tasks that must be performed on a contiguous block of a fixed or variable size. This could help us improve time complexity in so many problems by converting the nested loop solution into a single loop solution.

Example problems: Longest substring without repeating characters , Count distinct elements in every window , Max continuous series of 1s , Find max consecutive 1's in an array , etc.

Transform and Conquer Approach

This approach is based on transforming a coding problem into another coding problem with some particular property that makes the problem easier to solve. In other words, here we solve the problem is solved in two stages:

• Transformation stage: We transform the original problem into another easier problem to solve.
• Conquering stage: Now, we solve the transformed problem.

Example problems: Pre-sorting based algorithms (Finding the closest pair of points, checking whether all the elements in a given array are distinct, etc.)

Problem-solving using BFS and DFS Traversal

Most tree and graph problems can be solved using DFS and BFS traversal. If the problem is to search for something closer to the root (or source node), we can prefer BFS, and if we need to search for something in-depth, we can choose DFS.

Sometimes, we can use both BFS and DFS traversals when node order is not required. But in some cases, such things are not possible. We need to identify the use case of both traversals to solve the problems efficiently. For example, in binary tree problems:

• We use preorder traversal in a situation when we need to explore all the tree nodes before inspecting any leaves.
• Inorder traversal of BST generates the node's data in increasing order. So we can use inorder to solve several BST problems.
• We can use postorder traversal when we need to explore all the leaf nodes before inspecting any internal nodes.
• Sometimes, we need some specific information about some level. In this situation, BFS traversal helps us to find the output easily.

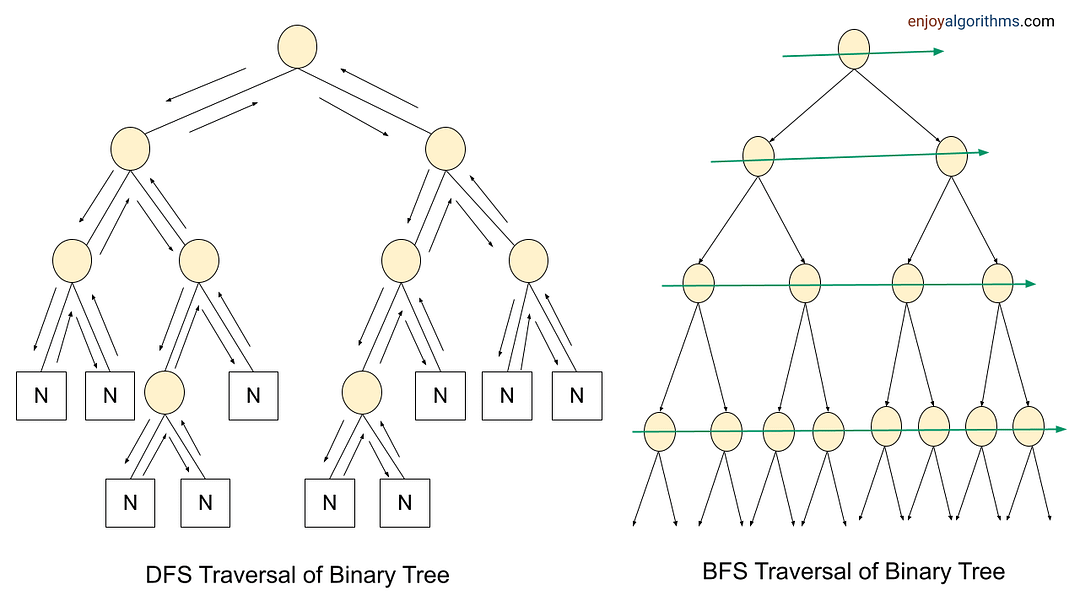
To solve tree and graph problems, sometimes we pass extra variables or pointers to the function parameters, use helper functions, use parent pointers, store some additional data inside the node, and use data structures like the stack, queue, and priority queue, etc.

Example problems: Find min depth of a binary tree , Merge two binary trees , Find the height of a binary tree , Find the absolute minimum difference in a BST , The kth largest element in a BST , Course scheduling problem , bipartite graph , Find the left view of a binary tree , etc.

Problem-solving using the Data Structures

The data structure is one of the powerful tools of problem-solving in algorithms. It helps us perform some of the critical operations efficiently and improves the time complexity of the solution. Here are some of the key insights:

• Many coding problems require an effcient way to perform the search, insert and delete operations. We can perform all these operations using the hash table in O(1) time average. It's a kind of time-memory tradeoff, where we use extra space to store elements in the hash table to improve performance.
• Sometimes we need to store data in the stack (LIFO order) or queue (FIFO order) to solve several coding problems. 
• Suppose there is a requirement to continuously insert or remove maximum or minimum element (Or element with min or max priority). In that case, we can use a heap (or priority queue) to solve the problem efficiently.
• Sometimes, we store data in Trie, AVL Tree, Segment Tree, etc., to perform some critical operations efficiently. 

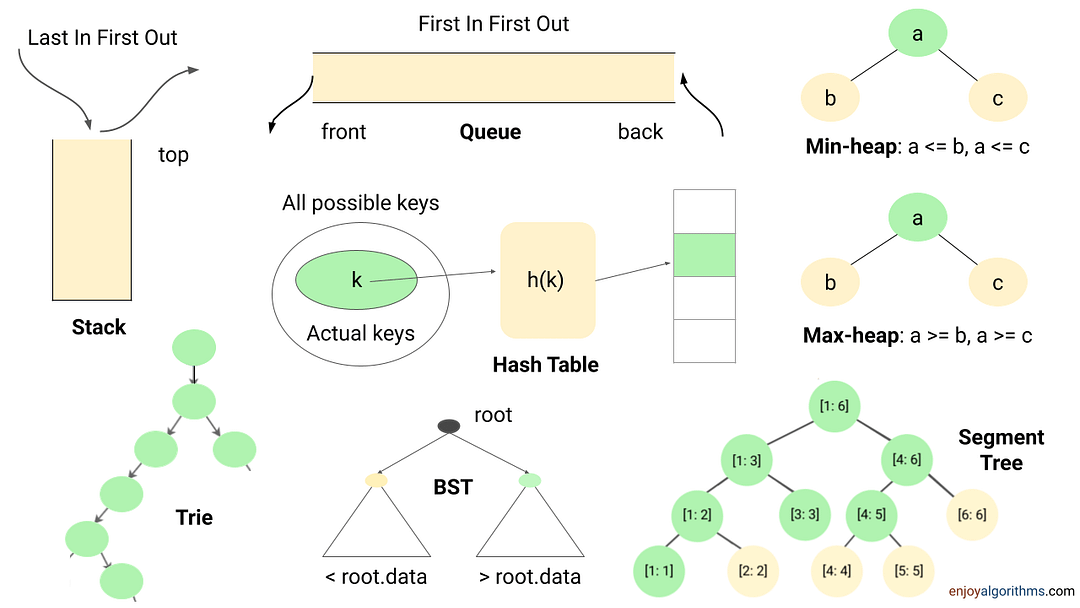
Example problems: Next greater element , Valid Parentheses , Largest rectangle in a histogram , Sliding window maximum , kth smallest element in an array , Top k frequent elements , Longest common prefix , Range sum query , Longest consecutive sequence , Check equal array , LFU cache , LRU cache , Counting sort

Dynamic Programming

Dynamic programming is one of the most popular techniques for solving problems with overlapping or repeated subproblems. Here rather than solving overlapping subproblems repeatedly, we solve each smaller subproblems only once and store the results in memory. We can solve a lot of optimization and counting problems using the idea of dynamic programming.

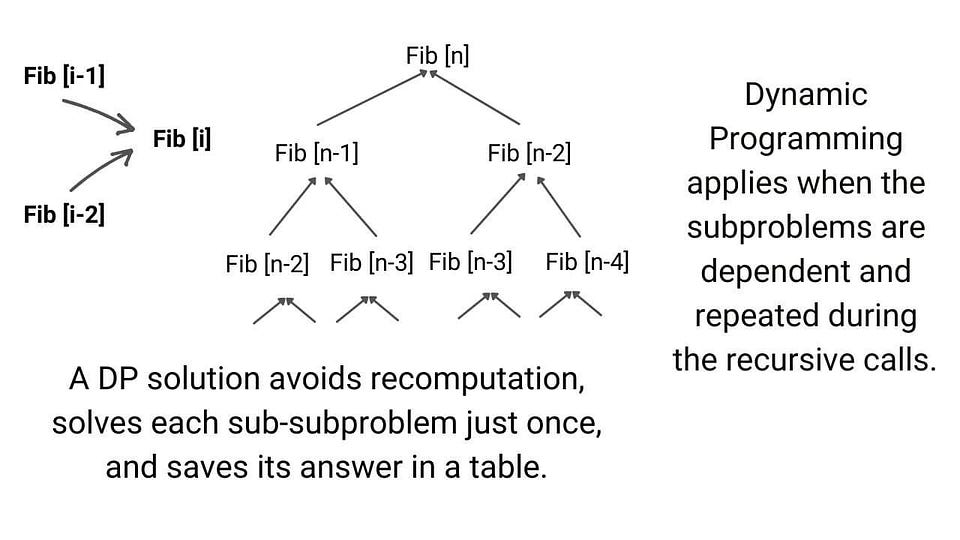
Example problems: Finding nth Fibonacci,  Longest Common Subsequence ,  Climbing Stairs Problem ,  Maximum Subarray Sum ,  Minimum number of Jumps to reach End ,  Minimum Coin Change

Greedy Approach

This solves an optimization problem by expanding a partially constructed solution until a complete solution is reached. We take a greedy choice at each step and add it to the partially constructed solution. This idea produces the optimal global solution without violating the problem’s constraints.

• The greedy choice is the best alternative available at each step is made in the hope that a sequence of locally optimal choices will yield a (globally) optimal solution to the entire problem.
• This approach works in some cases but fails in others. Usually, it is not difficult to design a greedy algorithm itself, but a more difficult task is to prove that it produces an optimal solution.

Example problems: Fractional Knapsack, Dijkstra algorithm, The activity selection problem

Exhaustive Search

This strategy explores all possibilities of solutions until a solution to the problem is found. Therefore, problems are rarely offered to a person to solve the problem using this strategy.

The most important limitation of exhaustive search is its inefficiency. As a rule, the number of solution candidates that need to be processed grows at least exponentially with the problem size, making the approach inappropriate not only for a human but often for a computer as well.

But in some situations, there is a need to explore all possible solution spaces in a coding problem. For example: Find all permutations of a string , Print all subsets , etc.

Backtracking

Backtracking is an improvement over the approach of exhaustive search. It is a method for generating a solution by avoiding unnecessary possibilities of the solutions! The main idea is to build a solution one piece at a time and evaluate each partial solution as follows:

• If a partial solution can be developed further without violating the problem’s constraints, it is done by taking the first remaining valid option at the next stage. ( Think! )
• Suppose there is no valid option at the next stage, i.e., If there is a violation of the problem constraint, the algorithm backtracks to replace the partial solution’s previous stage with the following option for that stage. ( Think! )

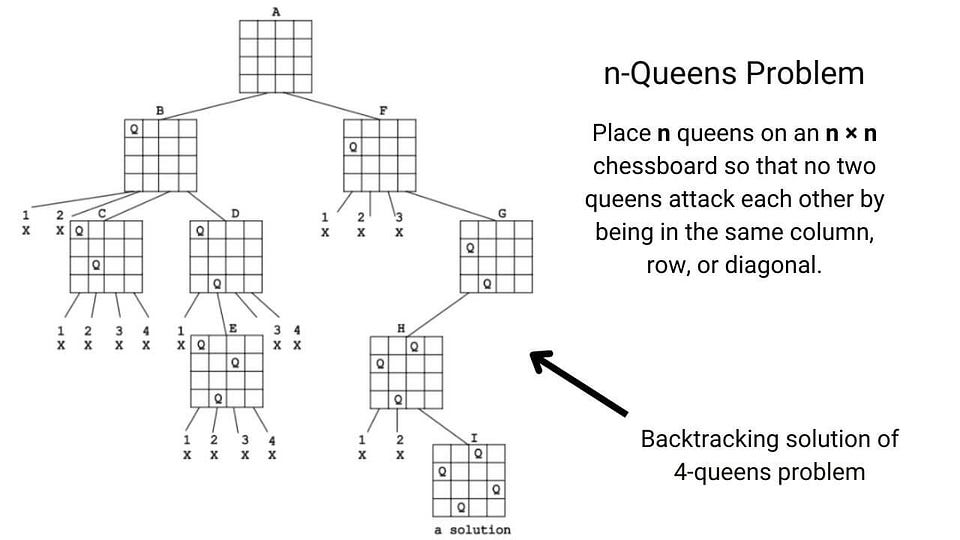
In simple words, backtracking involves undoing several wrong choices — the smaller this number, the faster the algorithm finds a solution. In the worst-case scenario, a backtracking algorithm may end up generating all the solutions as an exhaustive search, but this rarely happens!

Example problems: N-queen problem , Find all k combinations , Combination sum , Sudoku solver , etc.

Problem-solving using Bit manipulation and Numbers theory

Some of the coding problems are, by default, mathematical, but sometimes we need to identify the hidden mathematical properties inside the problem. So the idea of number theory and bit manipulation is helpful in so many cases.

Sometimes understanding the bit pattern of the input and processing data at the bit level help us design an efficient solution. The best part is that the computer performs each bit-wise operation in constant time. Even sometimes, bit manipulation can reduce the requirement of extra loops and improve the performance by a considerable margin.

Example problems: Reverse bits , Add binary string , Check the power of two , Find the missing number , etc.

Hope you enjoyed the blog. Later we will write a separate blog on each problem-solving approach. Enjoy learning, Enjoy algorithms!

Share Your Insights

Don’t fill this out if you’re human:

More from EnjoyAlgorithms

Self-paced courses and blogs, coding interview, machine learning, system design, oop concepts, our newsletter.

Subscribe to get well designed content on data structure and algorithms, machine learning, system design, object orientd programming and math.

©2023 Code Algorithms Pvt. Ltd.

All rights reserved.

MIT Sloan is the leader in research and teaching in AI. Dive in to discover why.

Which program is right for you?

Through intellectual rigor and experiential learning, this full-time, two-year MBA program develops leaders who make a difference in the world.

Earn your MBA and SM in engineering with this transformative two-year program.

A rigorous, hands-on program that prepares adaptive problem solvers for premier finance careers.

A 12-month program focused on applying the tools of modern data science, optimization and machine learning to solve real-world business problems.

Combine an international MBA with a deep dive into management science. A special opportunity for partner and affiliate schools only.

A doctoral program that produces outstanding scholars who are leading in their fields of research.

Bring a business perspective to your technical and quantitative expertise with a bachelor’s degree in management, business analytics, or finance.

Apply now and work for two to five years. We'll save you a seat in our MBA class when you're ready to come back to campus for your degree.

Executive Programs

The 20-month program teaches the science of management to mid-career leaders who want to move from success to significance.

A full-time MBA program for mid-career leaders eager to dedicate one year of discovery for a lifetime of impact.

A joint program for mid-career professionals that integrates engineering and systems thinking. Earn your master’s degree in engineering and management.

Non-degree programs for senior executives and high-potential managers.

A non-degree, customizable program for mid-career professionals.

The rise of the union-curious worker, and how to win them over

IKEA CEO: 3 ways to gain competitive advantage with sustainability

Consumers prefer early entrants in new markets, but 2nd movers can still win

Credit: Alejandro Giraldo

Ideas Made to Matter

How to use algorithms to solve everyday problems

Kara Baskin

May 8, 2017

How can I navigate the grocery store quickly? Why doesn’t anyone like my Facebook status? How can I alphabetize my bookshelves in a hurry? Apple data visualizer and MIT System Design and Management graduate Ali Almossawi solves these common dilemmas and more in his new book, “ Bad Choices: How Algorithms Can Help You Think Smarter and Live Happier ,” a quirky, illustrated guide to algorithmic thinking. 

For the uninitiated: What is an algorithm? And how can algorithms help us to think smarter?

An algorithm is a process with unambiguous steps that has a beginning and an end, and does something useful.

Algorithmic thinking is taking a step back and asking, “If it’s the case that algorithms are so useful in computing to achieve predictability, might they also be useful in everyday life, when it comes to, say, deciding between alternative ways of solving a problem or completing a task?” In all cases, we optimize for efficiency: We care about time or space.

Note the mention of “deciding between.” Computer scientists do that all the time, and I was convinced that the tools they use to evaluate competing algorithms would be of interest to a broad audience.

Why did you write this book, and who can benefit from it?

All the books I came across that tried to introduce computer science involved coding. My approach to making algorithms compelling was focusing on comparisons. I take algorithms and put them in a scene from everyday life, such as matching socks from a pile, putting books on a shelf, remembering things, driving from one point to another, or cutting an onion. These activities can be mapped to one or more fundamental algorithms, which form the basis for the field of computing and have far-reaching applications and uses.

I wrote the book with two audiences in mind. One, anyone, be it a learner or an educator, who is interested in computer science and wants an engaging and lighthearted, but not a dumbed-down, introduction to the field. Two, anyone who is already familiar with the field and wants to experience a way of explaining some of the fundamental concepts in computer science differently than how they’re taught.

I’m going to the grocery store and only have 15 minutes. What do I do?

Do you know what the grocery store looks like ahead of time? If you know what it looks like, it determines your list. How do you prioritize things on your list? Order the items in a way that allows you to avoid walking down the same aisles twice.

For me, the intriguing thing is that the grocery store is a scene from everyday life that I can use as a launch pad to talk about various related topics, like priority queues and graphs and hashing. For instance, what is the most efficient way for a machine to store a prioritized list, and what happens when the equivalent of you scratching an item from a list happens in the machine’s list? How is a store analogous to a graph (an abstraction in computer science and mathematics that defines how things are connected), and how is navigating the aisles in a store analogous to traversing a graph?

Nobody follows me on Instagram. How do I get more followers?

The concept of links and networks, which I cover in Chapter 6, is relevant here. It’s much easier to get to people whom you might be interested in and who might be interested in you if you can start within the ball of links that connects those people, rather than starting at a random spot.

You mention Instagram: There, the hashtag is one way to enter that ball of links. Tag your photos, engage with users who tag their photos with the same hashtags, and you should be on your way to stardom.

What are the secret ingredients of a successful Facebook post?

I’ve posted things on social media that have died a sad death and then posted the same thing at a later date that somehow did great. Again, if we think of it in terms that are relevant to algorithms, we’d say that the challenge with making something go viral is really getting that first spark. And to get that first spark, a person who is connected to the largest number of people who are likely to engage with that post, needs to share it.

With [my first book], “Bad Arguments,” I spent a month pouring close to $5,000 into advertising for that project with moderate results. And then one science journalist with a large audience wrote about it, and the project took off and hasn’t stopped since.

What problems do you wish you could solve via algorithm but can’t?

When we care about efficiency, thinking in terms of algorithms is useful. There are cases when that’s not the quality we want to optimize for — for instance, learning or love. I walk for several miles every day, all throughout the city, as I find it relaxing. I’ve never asked myself, “What’s the most efficient way I can traverse the streets of San Francisco?” It’s not relevant to my objective.

Algorithms are a great way of thinking about efficiency, but the question has to be, “What approach can you optimize for that objective?” That’s what worries me about self-help: Books give you a silver bullet for doing everything “right” but leave out all the nuances that make us different. What works for you might not work for me.

Which companies use algorithms well?

When you read that the overwhelming majority of the shows that users of, say, Netflix, watch are due to Netflix’s recommendation engine, you know they’re doing something right.

Related Articles

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

What Is an Algorithm in Psychology?

Definition, Examples, and Uses

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

 James Lacy, MLS, is a fact-checker and researcher.

How Does an Algorithm Work?

Examples of algorithms.

• Reasons to Use Algorithms
• Potential Pitfalls

Algorithms vs. Heuristics

When solving a problem , choosing the right approach is often the key to arriving at the best solution. In psychology, one of these problem-solving approaches is known as an algorithm. While often thought of purely as a mathematical term, the same type of process can be followed in psychology to find the correct answer when solving a problem or making a decision.

An algorithm is a defined set of step-by-step procedures that provides the correct answer to a particular problem. By following the instructions correctly, you are guaranteed to arrive at the right answer.

At a Glance

Algorithms involve following specific steps in order to reach a solution to a problem. They can be a great tool when you need an accurate solution but tend to be more time-consuming than other methods.

This article discusses how algorithms are used as an approach to problem-solving. It also covers how psychologists compare this approach to other problem-solving methods.

An algorithm is often expressed in the form of a graph, where a square represents each step. Arrows then branch off from each step to point to possible directions that you may take to solve the problem.

In some cases, you must follow a particular set of steps to solve the problem. In other instances, you might be able to follow different paths that will all lead to the same solution.

Algorithms are essential step-by-step approaches to solving a problem. Rather than guessing or using trial-and-error, this approach is more likely to guarantee a specific solution. 

Using an algorithm can help you solve day-to-day problems you face, but it can also help mental health professionals find ways to help people cope with mental health problems.

For example, a therapist might use an algorithm to treat a person experiencing something like anxiety. Because the therapist knows that a particular approach is likely to be effective, they would recommend a series of specific, focused steps as part of their intervention.

There are many different examples of how algorithms can be used in daily life. Some common ones include:

• A recipe for cooking a particular dish
• The method a search engine uses to find information on the internet
• Instructions for how to assemble a bicycle
• Instructions for how to solve a Rubik's cube
• A process to determine what type of treatment is most appropriate for certain types of mental health conditions

Doctors and mental health professionals often use algorithms to diagnose mental disorders . For example, they may use a step-by-step approach when they evaluate people.

This might involve asking the individual about their symptoms and their medical history. The doctor may also conduct lab tests, physical exams, or psychological assessments.

Using this information, they then utilize the "Diagnostic and Statistical Manual of Mental Disorders" (DSM-5-TR) to make a diagnosis.

Reasons to Use Algorithms in Psychology

The upside of using an algorithm to solve a problem or make a decision is that yields the best possible answer every time. There are situations where using an algorithm can be the best approach:

When Accuracy Is Crucial

Algorithms can be particularly useful in situations when accuracy is critical. They are also a good choice when similar problems need to be frequently solved.

Computer programs can often be designed to speed up this process. Data then needs to be placed in the system so that the algorithm can be executed for the correct solution.

Artificial intelligence may also be a tool for making clinical assessments in healthcare situations.

When Each Decision Needs to Follow the Same Process

Such step-by-step approaches can be useful in situations where each decision must be made following the same process. Because the process follows a prescribed procedure, you can be sure that you will reach the correct answer each time.

Potential Pitfalls When Using Algorithms

The downside of using an algorithm to solve the problem is that this process tends to be very time-consuming.

So if you face a situation where a decision must be made very quickly, you might be better off using a different problem-solving strategy.

For example, an emergency room doctor making a decision about how to treat a patient could use an algorithm approach. However, this would be very time-consuming and treatment needs to be implemented quickly.

In this instance, the doctor would instead rely on their expertise and past experiences to very quickly choose what they feel is the right treatment approach.

Algorithms can sometimes be very complex and may only apply to specific situations. This can limit their use and make them less generalizable when working with larger populations.

Algorithms can be a great problem-solving choice when the answer needs to be 100% accurate or when each decision needs to follow the same process. A different approach might be needed if speed is the primary concern.

In psychology, algorithms are frequently contrasted with heuristics . Both can be useful when problem-solving, but it is important to understand the differences between them.

What Is a Heuristic?

A heuristic is a mental shortcut that allows people to quickly make judgments and solve problems.

These mental shortcuts are typically informed by our past experiences and allow us to act quickly. However, heuristics are really more of a rule-of-thumb; they don't always guarantee a correct solution.

So how do you determine when to use a heuristic and when to use an algorithm? When problem-solving, deciding which method to use depends on the need for either accuracy or speed.

When to Use an Algorithm

If complete accuracy is required, it is best to use an algorithm. By using an algorithm, accuracy is increased and potential mistakes are minimized.

If you are working in a situation where you absolutely need the correct or best possible answer, your best bet is to use an algorithm. When you are solving problems for your math homework, you don't want to risk your grade on a guess.

By following an algorithm, you can ensure that you will arrive at the correct answer to each problem.

When to Use a Heuristic

On the other hand, if time is an issue, then it may be best to use a heuristic. Mistakes may occur, but this approach allows for speedy decisions when time is of the essence.

Heuristics are more commonly used in everyday situations, such as figuring out the best route to get from point A to point B. While you could use an algorithm to map out every possible route and determine which one would be the fastest, that would be a very time-consuming process. Instead, your best option would be to use a route that you know has worked well in the past.

Psychologists who study problem-solving have described two main processes people utilize to reach conclusions: algorithms and heuristics. Knowing which approach to use is important because these two methods can vary in terms of speed and accuracy.

While each situation is unique, you may want to use an algorithm when being accurate is the primary concern. But if time is of the essence, then an algorithm is likely not the best choice.

Lang JM, Ford JD, Fitzgerald MM. An algorithm for determining use of trauma-focused cognitive-behavioral therapy . Psychotherapy (Chic) . 2010;47(4):554-69. doi:10.1037/a0021184

Stein DJ, Shoptaw SJ, Vigo DV, et al. Psychiatric diagnosis and treatment in the 21st century: paradigm shifts versus incremental integration .  World Psychiatry . 2022;21(3):393-414. doi:10.1002/wps.20998

Bobadilla-Suarez S, Love BC. Fast or frugal, but not both: decision heuristics under time pressure . J Exp Psychol Learn Mem Cogn . 2018;44(1):24-33. doi:10.1037/xlm0000419

Giordano C, Brennan M, Mohamed B, Rashidi P, Modave F, Tighe P. Accessing artificial intelligence for clinical decision-making .  Front Digit Health . 2021;3:645232. doi:10.3389/fdgth.2021.645232

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."