algebra problem solving gcse

PMT Education is looking for a full-time Customer Support Specialist

Get £10 off your first lesson on PMT Tuition using the code PMTSEPT10

Edexcel Algebra Questions by Topic

University of Oxford - MMath Mathematics

Experienced Maths and Further Maths tutor

On this page you can find past paper questions separated by topic and topic tests, for both Foundation and Higher tiers. All question sets are taken from past papers, except for the third set, which features topic tests. Set 5 includes the latest past paper questions from 2021 to 2023. Set 4 is from 2017-2021 and is the only set with video solutions .

It is recommended to start with Set 4 and Set 5, and if you need additional practice, you can work on sets 1-3 afterwards.

For notes, worksheets and their solutions, visit the GCSE Algebra Revision page. Full past papers and model solutions can be found on the Paper 1 , Paper 2 and Paper 3 pages.

Notation Vocabulary and Manipulation

• Algebraic Proofs (FH)
• Deriving Expressions (F)
• Deriving Expressions (FH)
• Expanding Equations (F)
• Expanding Expressions (FH)
• Factorising Equations (F)
• Factorising Expressions (FH)
• Forming Equations (F)
• Forming Equations (FH)
• Input-Output (F)
• Manipulation of Formulae (F)
• Manipulation of Formulae (FH)
• Simplifying Expressions (F)
• Simplifying Expressions (FH)
• Solving Using Indices (FH)
• Substitution (F)
• Substitution Into Equations (FH)
• Sequence of Diagrams (FH)
• Sequence of Numbers (FH)
• Sequences of Diagrams (F)
• Sequences of Numbers (F)
• Conversion Graphs (F)
• Conversion Graphs (FH)
• Coordinates in 3D (FH)
• Distance-Time Graphs (F)
• Distance-Time Graphs (FH)
• Exponential Growth and Decay (FH)
• Gradients of Straight Lines (FH)
• Graphs of Circles (FH)
• Graphs of Linear Equations (FH)
• Graphs of Quadratic Equations (FH)
• Graphs of Trigonometrical Functions (FH)
• Line Graphs (F)
• Line Graphs of Real Situations (FH)
• Transformation of Graphs (FH)
• Using y=mx+c (FH)

Solving Equations and Inequalities

• Solving Inequalities (F)
• Solving Inequalities (FH)
• Solving Linear Equations (F)
• Solving Linear Equations (FH)
• Solving Quadratic Equations (F)
• Solving Quadratic Equations (FH)
• Solving by Trial and Improvement (FH)
• Algebraic Proofs (H)
• Expanding Equations (H)
• Factorising Expressions (H)
• Forming Equations (H)
• Manipulation of Formulae (H)
• Simplifying Expressions (H)
• Solving Algebraic Fraction Equations (H)
• Solving Algebraic Fractions (H)
• Solving Using Indices (H)
• Substitution (H)
• Exponential Growth and Decay (H)
• Gradients of Straight Lines (H)
• Graphs of Circles (H)
• Graphs of Linear Equations (H)
• Graphs of Quadratic Equations (H)
• Graphs of Trigonometrical Functions (H)
• Line Graphs of Real Situations (H)
• Transformation of Graphs (H)
• Using y=mx+c (H)
• Solving Inequalities (H)
• Solving Simultaneous Equations (H)
• Expanding Expressions (F)
• Simplfying Equations (FH) 2
• Simplifying Equations (F)
• Simplifying Equations (FH) 1
• Substituting Into Equations (F)
• Substituting Into Equations (FH)
• Sequences (F)
• Sequences (FH)
• Distance-Time and Travel Graphs (F)
• Distance-Time and Travel Graphs (FH)
• Graphs of Linear Equations (F)
• Solving Simultaneous Equations (FH)
• Trial and Improvement (FH)
• Deriving Expressions (H)
• Expanding Expressions (H)
• Functions (H)
• Simplfying Equations (H) 2
• Simplifying Equations (H) 1
• Substituting Into Equations (H)
• Sequences (H)
• Graphs of Cubic Equations (H)
• Graphs of Reciprocal Equations (H)
• Transformation of Functions (H)
• Solving Linear Equations (H)
• Complex Graphs and Simultaneous Equations (F)
• Equations and Inequalities (F)
• Manipulating Expressions (F)
• Quadratic Equations and Graphs (F)
• Real-Life and Algebraic Linear Graphs (F)
• Algebra (H)
• Direct and Indirect Proportion (H)
• Direct and Inverse Proportion and Compound Measures (H)
• Graphs and Coordinate Geometry (H)
• Manipulating Expressions (H)
• Quadratic, Cubic and Other Graphs (H)
• Quadratics and Complex Graphs (H)
• Quadratics, Inequalities and Simultaneous Equations (H)

Notation, Vocabulary and Manipulation

• Inputs and Outputs (F)
• Substitution into Equations (F)
• Coordinates (F)
• Cubic and Reciprocal Graphs (F)
• Equations of Straight Lines (F)
• Graphs of Quadratic Equations (F)
• Interpreting Gradients (F)
• Simultaneous Equations (F)
• Solving Quadratic Equations(F)
• Algebraic Fractions (H)
• Algebraic Proof (H)
• Expanding Triple Brackets (H)
• Factorising Equations (H)
• Functions (Composite or Inverse) (H)
• Substitution into Equations (H)
• Geometric Progression (H)
• Circle Equations and Tangents (H)
• Coordinates (H)
• Cubic and Reciprocal Graphs (H)
• Distance-Time Graphs (H)
• Equations of Straight Lines (H)
• Exponential and Trigonometric Graphs (H)
• Interpreting Gradients (H)
• Parallel or Perpendicular Lines (H)
• Simultaneous Equations on Graphs (H)
• Translations and Reflections of Functions (H)
• Velocity-Time Graphs (H)
• Completing the Square (H)
• Inequalities (H)
• Inequalities on Graphs (H)
• Iteration (H)
• Quadratic Sequences (H)
• Simultaneous Equations (H)
• Solve by Factorising (H)
• Solving Quadratic Equations (H)

Notation, Vocabulary and Manipulation || Sequences || Graphs || Solving Equations and Inequalities

Question Papers

• Deriving Expressions (F) QP
• Expanding Equations (F) QP
• Factorising Equations (F) QP
• Forming Equations (F) QP
• Inputs and Outputs (F) QP
• Manipulation of Formulae (F) QP
• Simplifying Expressions (F) QP
• Substitution into Equations (F) QP

Mark Schemes

• Deriving Expressions (F) MS
• Expanding Equations (F) MS
• Factorising Equations (F) MS
• Forming Equations (F) MS
• Inputs and Outputs (F) MS
• Manipulation of Formulae (F) MS
• Simplifying Expressions (F) MS
• Substitution into Equations (F) MS

Model Answers

• Deriving Expressions (F) MA
• Expanding Equations (F) MA
• Factorising Equations (F) MA
• Forming Equations (F) MA
• Inputs and Outputs (F) MA
• Manipulation of Formulae (F) MA
• Simplifying Expressions (F) MA
• Substitution into Equations (F) MA
• Sequences (F) QP
• Sequences (F) MS
• Sequences (F) MA
• Conversion Graphs (F) QP
• Coordinates (F) QP
• Cubic and Reciprocal Graphs (F) QP
• Distance-time Graphs (F) QP
• Equations of Straight Lines (F) QP
• Graphs of Circles (F) QP
• Graphs of Linear Equations (F) QP
• Graphs of Quadratic Equations (F) QP
• Travel Graphs (F) QP
• Conversion Graphs (F) MS
• Coordinates (F) MS
• Cubic and Reciprocal Graphs (F) MS
• Distance-time Graphs (F) MS
• Equations of Straight Lines (F) MS
• Graphs of Circles (F) MS
• Graphs of Linear Equations (F) MS
• Graphs of Quadratic Equations (F) MS
• Travel Graphs (F) MS
• Conversion Graphs (F) MA
• Coordinates (F) MA
• Cubic and Reciprocal Graphs (F) MA
• Distance-time Graphs (F) MA
• Equations of Straight Lines (F) MA
• Graphs of Circles (F) MA
• Graphs of Linear Equations (F) MA
• Graphs of Quadratic Equations (F) MA
• Travel Graphs (F) MA
• Inequalities (F) QP
• Simultaneous Equations (F) QP
• Solving Linear Equations (F) QP
• Solving using Indices (F) QP
• Inequalities (F) MS
• Simultaneous Equations (F) MS
• Solving Linear Equations (F) MS
• Solving using Indices (F) MS
• Inequalities (F) MA
• Simultaneous Equations (F) MA
• Solving Linear Equations (F) MA
• Solving using Indices (F) MA
• Algebraic Fractions (H) QP
• Algebraic Proof (H) QP
• Deriving Expressions (H) QP
• Expanding Equations (H) QP
• Expanding Triple Brackets (H) QP
• Factorising Equations (H) QP
• Functions (Composite or Inverse) (H) QP
• Manipulation of Formulae (H) QP
• Simplifying Expressions (H) QP
• Solving using Indices (H) QP
• Substitution into Equations (H) QP
• Algebraic Fractions (H) MS
• Algebraic Proof (H) MS
• Deriving Expressions (H) MS
• Expanding Equations (H) MS
• Expanding Triple Brackets (H) MS
• Factorising Equations (H) MS
• Functions (Composite or Inverse) (H) MS
• Manipulation of Formulae (H) MS
• Simplifying Expressions (H) MS
• Solving using Indices (H) MS
• Substitution into Equations (H) MS
• Algebraic Fractions (H) MA
• Algebraic Proof (H) MA
• Deriving Expressions (H) MA
• Expanding Equations (H) MA
• Expanding Triple Brackets (H) MA
• Factorising Equations (H) MA
• Functions (Composite or Inverse) (H) MA
• Manipulation of Formulae (H) MA
• Simplifying Expressions (H) MA
• Solving using Indices (H) MA
• Substitution into Equations (H) MA
• Geometric Progression (H) QP
• Sequences (H) QP
• Geometric Progression (H) MS
• Sequences (H) MS
• Geometric Progression (H) MA
• Sequences (H) MA
• Circles Equations and Tangents (H) QP
• Coordinates (H) QP
• Cubic and Reciprocal Graphs (H) QP
• Distance-time Graphs (H) QP
• Equations of Straight Lines (H) QP
• Exponential and Trigonometric Graphs (H) QP
• Graphs of Circles (H) QP
• Graphs of Linear Equations (H) QP
• Graphs of Quadratic Equations (H) QP
• Interpreting Gradients (H) QP
• Simultaneous Equations on Graphs (H) QP
• Translations and Reflections of Functions (H) QP
• Velocity-time graphs (H) QP
• Circle Equations and Tangents (H) MS
• Coordinates (H) MS
• Cubic and Reciprocal Graphs (H) MS
• Distance-time Graphs (H) MS
• Equations of Straight Lines (H) MS
• Exponential and Trigonometric Graphs (H) MS
• Graphs of Circles (H) MS
• Graphs of Linear Equations (H) MS
• Graphs of Quadratic Equations (H) MS
• Interpreting Gradients (H) MS
• Simultaneous Equations on Graphs (H) MS
• Translations and Reflections of Functions (H) MS
• Velocity-time graphs (H) MS
• Circle Equations and Tangents (H) MA
• Coordinates (H) MA
• Cubic and Reciprocal Graphs (H) MA
• Distance-time Graphs (H) MA
• Equations of Straight Lines (H) MA
• Exponential and Trigonometric Graphs (H) MA
• Graphs of Circles (H) MA
• Graphs of Linear Equations (H) MA
• Graphs of Quadratic Equations (H) MA
• Interpreting Gradients (H) MA
• Simultaneous Equations on Graphs (H) MA
• Translations and Reflections of Functions (H) MA
• Velocity-time graphs (H) MA
• Completing the square (H) QP
• Gradients of Straight Lines (H) QP
• Inequalities (H) QP
• Inequalities on Graphs (H) QP
• Iteration (H) QP
• Quadratic Formula (H) QP
• Quadratic Inequalities (H) QP
• Quadratics Sequences (H) QP
• Simultaneous Equations (H) QP
• Solving Quadratic Equations (H) QP
• Completing the square (H) MS
• Gradients of Straight lines (H) MS
• Inequalities (H) MS
• Inequalities on Graphs (H) MS
• Iteration (H) MS
• Quadratic Formula (H) MS
• Quadratic Inequalities (H) MS
• Quadratic Sequences (H) MS
• Simultaneous Equations (H) MS
• Solving Quadratic Equations (H) MS
• Completing the square (H) MA
• Gradients of Straight lines (H) MA
• Inequalities (H) MA
• Inequalities on Graphs (H) MA
• Iteration (H) MA
• Quadratic Formula (H) MA
• Quadratic Inequalities (H) MA
• Quadratic Sequences (H) MA
• Simultaneous Equations (H) MA
• Solving Quadratic Equations (H) MA

Connect with PMT Education!

• Revision Courses
• Past Papers
• Solution Banks
• University Admissions
• Numerical Reasoning
• Legal Notices

The resources on this page will hopefully help you teach AO2 and AO3 of the new GCSE specification - problem solving and reasoning.

This brief lesson is designed to lead students into thinking about how to solve mathematical problems. It features ideas of strategies to use, clear steps to follow and plenty of opportunities for discussion.

The PixiMaths problem solving booklets are aimed at "crossover" marks (questions that will be on both higher and foundation) so will be accessed by most students. The booklets are collated Edexcel exam questions; you may well recognise them from elsewhere. Each booklet has 70 marks worth of questions and will probably last two lessons, including time to go through answers with your students. There is one for each area of the new GCSE specification and they are designed to complement the PixiMaths year 11 SOL.

These problem solving starter packs are great to support students with problem solving skills. I've used them this year for two out of four lessons each week, then used Numeracy Ninjas as starters for the other two lessons.  When I first introduced the booklets, I encouraged my students to use scaffolds like those mentioned here , then gradually weaned them off the scaffolds. I give students some time to work independently, then time to discuss with their peers, then we go through it as a class. The levels correspond very roughly to the new GCSE grades.

Some of my favourite websites have plenty of other excellent resources to support you and your students in these assessment objectives.

@TessMaths has written some great stuff for BBC Bitesize.

There are some intersting though-provoking problems at Open Middle.

I'm sure you've seen it before, but if not, check it out now! Nrich is where it's at if your want to provide enrichment and problem solving in your lessons.

MathsBot  by @StudyMaths has everything, and if you scroll to the bottom of the homepage you'll find puzzles and problem solving too.

I may be a little biased because I love Edexcel, but these question packs are really useful.

The UKMT has a mentoring scheme that provides fantastic problem solving resources , all complete with answers.

I have only recently been shown Maths Problem Solving and it is awesome - there are links to problem solving resources for all areas of maths, as well as plenty of general problem solving too. Definitely worth exploring!

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

In order to access this I need to be confident with:

This topic is relevant for:

Solving Equations

Here we break down everything you need to know about solving equations. You’ll learn what linear and quadratic algebraic equations are, and how to solve all the different types of them.

At the end you’ll find solving equations worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is an equation?

An equation is a mathematical expression that contains an equals sign .

There are two sides to an equation, with the left side being equal to the right side.

Equations will often involve algebra and contain unknowns (variables) which we often represent with letters such as x or y .

We can solve simple equations and more complicated equations to work out the value of these unknowns; they could involve fractions, decimals or integers.

Step-by-step guide: Forming and solving equations

Solving equations worksheets

Get your free solving equations worksheet of 20+ questions and answers. Includes reasoning and applied questions.

How to solve equations

In order to solve equations, we need to work out the value of the unknown variable by adding, subtracting, multiplying or dividing both sides of the equation by the same value.

To solve equations step by step

• Multiply out any brackets using the distributive property
• Multiply or divide the same number to both sides of the equation
• Add or subtract the same number to both sides of the equation

In GCSE Maths there are two main types of equations that we need to solve: linear equations and quadratic equations. Methods of solving each are provided below.

Explain how to solve equations

Solving equations methods

Within solving equations, you will find lessons on linear equations and quadratic equations.

Each method of solving equations is summarised below. For detailed examples, practice questions and worksheets on each one follow the links to the step by step guides.

1. Linear equations

There are 5 main types of linear equations we can solve.

Example of solving an equation with:

• One unknown

2 Unknown on both sides

3 With brackets

4 With fractions

Step-by-step guide: Equations with fractions

5 Powers (exponents) and roots

We can check that our solution is correct by substituting it into the original equation.

Step-by-step guide: Linear equations

Step-by-step guide: Iteration maths

2. Quadratic equations

There are 4 main ways to solve quadratic equations.

Example of solving a quadratic equation by:

• Factorising

Step-by-step guide: Solving quadratic equations by factorising

2 Quadratic Formula

Step-by-step guide: Quadratic formula

3 Complete the square

Step-by-step guide: Completing the square

4 Graphically

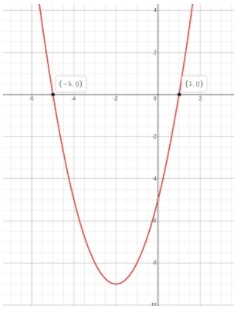
The solutions/roots are found when the graph equals 0 (crosses the x -axis).

Step-by-step guide: Solving quadratic equations graphically

See also: Quadratic equations

Practice solving equations questions

1. Solve: 4x-2=14

Add 2 to both sides

Divide both sides by   4

2. Solve: 3x-8=x+6

Add 8 to both sides

Subtract x from both sides

Divide both sides by 2

3. Solve: 3(x+3)=2(x-2)

Expanding the brackets

Subtract 9 from both sides

Subtract 2x from both sides

4. Solve: \frac{2 x+2}{3}=\frac{x-3}{2}

Multiply by 6 (the lowest common denominator) and simplify

Expand the brackets

Subtract 4 from both sides

Subtract 3x from both sides

5. Solve: \frac{3 x^{2}}{2}=24

Multiply both sides by 2

Divide both sides by 3

Square root both sides

6. Solve by factorising: x^{2}-13 x+30=0

Factorise as a double bracket

Set each bracket equal to zero and solve, hence

x=3 or x=10

7. Solve by factorising: 2 x^{2}+3 x-20=0

8. (H) Solve by using the quadratic formula:  x^{2}-4 x-3=0 give your answer to 3 significant figures

Substitution into the quadratic formula gives

x=\frac{-(-4)+\sqrt{(-4)^{2}-4(1)(-3)}}{2(1)} \quad \quad \quad \; x=\frac{-(-4)-\sqrt{(-4)^{2}-4(1)(-3)}}{2(1)} \\ x=2+\sqrt{7} \quad \quad \quad \quad \quad \quad \quad \quad x=2-\sqrt{7} \\ x=4.65 \; (3.5 . f) \quad \quad \quad\quad \quad \quad x=-0.646 \; (3.s.f)

9. (H) Solve by using the quadratic formula:  2 x^{2}+4 x-4=0 give your answer to 3 significant figures

x=\frac{-(4)+\sqrt{(4)^{2}-4(2)(-4)}}{2(2)} \quad \quad \quad \; x=\frac{-(4)+\sqrt{(4)^{2}-4(2)(-4)}}{2(2)} \\ x=-1+\sqrt{3} \quad \quad \quad \quad \quad \quad \quad \quad x=-1-\sqrt{3} \\ x=0.732 \; (3.s.f) \quad \quad \quad \quad \quad \quad x=-2.73 \; (3.s.f)

10. (H) Solve by completing the square: x^{2}-6 x+5=0

Completing the square

Add 4 to both sides

Add 3 to both sides

So x=5, \; x=1

Solving equations GCSE questions

1. Solve: 4y = 36

2. Solve: x 2 − 5x − 24 = 0

x = − 3, x = 8

3. Solve: 7y − 8 = 13

Learning checklist

• Use algebraic methods to solve linear equations
• Solve quadratic equations algebraically by factorising
• Solve quadratic equations algebraically by completing the square (H)
• Solve quadratic equations algebraically by using the quadratic formula (H)
• Solve quadratic equations by finding approximate solutions using a graph

The next lessons are

• Quadratic equations
• Simultaneous equations
• Rearranging equations

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Part of Maths

Algebraic expressions - Edexcel

Letters can be used to stand for unknown values or values that can change. Formulas can be written and equations solved to find solutions to a range of problems in science and engineering.

Algebraic formulae - Edexcel

Formulae are used in everyday life, from working out areas and volumes of shapes to converting units of measurement. Knowing how to use and rearrange formulae are very useful skills.

Solving linear equations - Edexcel

Forming, using and solving equations are skills needed in many different situations. From balancing accounts to making sense of a mobile phone bill, solving equations is a vital skill.

Solving simultaneous equations - Edexcel

Simultaneous equations require algebraic skills to find the values of letters within two or more equations. They are called simultaneous equations because the equations are solved at the same time.

Solving quadratic equations - Edexcel

Solve quadratic equations by factorising, using formulae and completing the square. Each method also provides information about the corresponding quadratic graph.

Algebraic fractions - Edexcel

Algebraic expressions in fraction form are rational. Methods of adding, subtracting, multiplying and dividing fractions plus expanding and factorising can be used to simplify rational expressions.

Inequalities - Edexcel

Inequalities show the relationship between two expressions that are not equal to one another. Inequalities are useful when projecting profits and breakeven figures.

Sequences - Edexcel

Sequences can be linear, quadratic or practical and based on real-life situations. Finding general rules helps find terms in sequences.

Straight line graphs - Edexcel

Graphs show the relationship between two variables and are often seen in newspapers and the media. People who work in professions involving maths and science commonly use graphs.

Other graphs - Edexcel

The most commonly occurring graphs are quadratic, cubic, reciprocal, exponential and circle graphs. Their equations can be used to plot their shape.

Transformation of curves - Higher - Edexcel

Functions of graphs can be transformed to show shifts and reflections. Graphic designers and 3D modellers use transformations of graphs to design objects and images.

Using and interpreting graphs - Edexcel

Using graphs is not just about reading off values. In real-life contexts, the intercept, gradient and area underneath the graph can have important meanings such as a fixed charge, speed or distance.

Maths: Exam-style questions

Personalise your Bitesize!

Jobs that use Maths

Skillswise: Maths

Radio 4: Maths collection

Save My Exams

• External link External link
• Subscription Subscription

Pearson Education