- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive

Factor Analysis Guide with an Example
By Jim Frost 20 Comments
What is Factor Analysis?
Factor analysis uses the correlation structure amongst observed variables to model a smaller number of unobserved, latent variables known as factors. Researchers use this statistical method when subject-area knowledge suggests that latent factors cause observable variables to covary. Use factor analysis to identify the hidden variables.
Analysts often refer to the observed variables as indicators because they literally indicate information about the factor. Factor analysis treats these indicators as linear combinations of the factors in the analysis plus an error. The procedure assesses how much of the variance each factor explains within the indicators. The idea is that the latent factors create commonalities in some of the observed variables.
For example, socioeconomic status (SES) is a factor you can’t measure directly. However, you can assess occupation, income, and education levels. These variables all relate to socioeconomic status. People with a particular socioeconomic status tend to have similar values for the observable variables. If the factor (SES) has a strong relationship with these indicators, then it accounts for a large portion of the variance in the indicators.
The illustration below illustrates how the four hidden factors in blue drive the measurable values in the yellow indicator tags.

Researchers frequently use factor analysis in psychology, sociology, marketing, and machine learning.
Let’s dig deeper into the goals of factor analysis, critical methodology choices, and an example. This guide provides practical advice for performing factor analysis.
Analysis Goals
Factor analysis simplifies a complex dataset by taking a larger number of observed variables and reducing them to a smaller set of unobserved factors. Anytime you simplify something, you’re trading off exactness with ease of understanding. Ideally, you obtain a result where the simplification helps you better understand the underlying reality of the subject area. However, this process involves several methodological and interpretative judgment calls. Indeed, while the analysis identifies factors, it’s up to the researchers to name them! Consequently, analysts debate factor analysis results more often than other statistical analyses.
While all factor analysis aims to find latent factors, researchers use it for two primary goals. They either want to explore and discover the structure within a dataset or confirm the validity of existing hypotheses and measurement instruments.
Exploratory Factor Analysis (EFA)
Researchers use exploratory factor analysis (EFA) when they do not already have a good understanding of the factors present in a dataset. In this scenario, they use factor analysis to find the factors within a dataset containing many variables. Use this approach before forming hypotheses about the patterns in your dataset. In exploratory factor analysis, researchers are likely to use statistical output and graphs to help determine the number of factors to extract.
Exploratory factor analysis is most effective when multiple variables are related to each factor. During EFA, the researchers must decide how to conduct the analysis (e.g., number of factors, extraction method, and rotation) because there are no hypotheses or assessment instruments to guide them. Use the methodology that makes sense for your research.
For example, researchers can use EFA to create a scale, a set of questions measuring one factor. Exploratory factor analysis can find the survey items that load on certain constructs.
Confirmatory Factor Analysis (CFA)
Confirmatory factor analysis (CFA) is a more rigid process than EFA. Using this method, the researchers seek to confirm existing hypotheses developed by themselves or others. This process aims to confirm previous ideas, research, and measurement and assessment instruments. Consequently, the nature of what they want to verify will impose constraints on the analysis.
Before the factor analysis, the researchers must state their methodology including extraction method, number of factors, and type of rotation. They base these decisions on the nature of what they’re confirming. Afterwards, the researchers will determine whether the model’s goodness-of-fit and pattern of factor loadings match those predicted by the theory or assessment instruments.
In this vein, confirmatory factor analysis can help assess construct validity. The underlying constructs are the latent factors, while the items in the assessment instrument are the indicators. Similarly, it can also evaluate the validity of measurement systems. Does the tool measure the construct it claims to measure?
For example, researchers might want to confirm factors underlying the items in a personality inventory. Matching the inventory and its theories will impose methodological choices on the researchers, such as the number of factors.
We’ll get to an example factor analysis in short order, but first, let’s cover some key concepts and methodology choices you’ll need to know for the example.
Learn more about Validity and Construct Validity .
In this context, factors are broader concepts or constructs that researchers can’t measure directly. These deeper factors drive other observable variables. Consequently, researchers infer the properties of unobserved factors by measuring variables that correlate with the factor. In this manner, factor analysis lets researchers identify factors they can’t evaluate directly.
Psychologists frequently use factor analysis because many of their factors are inherently unobservable because they exist inside the human brain.
For example, depression is a condition inside the mind that researchers can’t directly observe. However, they can ask questions and make observations about different behaviors and attitudes. Depression is an invisible driver that affects many outcomes we can measure. Consequently, people with depression will tend to have more similar responses to those outcomes than those who are not depressed.
For similar reasons, factor analysis in psychology often identifies and evaluates other mental characteristics, such as intelligence, perseverance, and self-esteem. The researchers can see how a set of measurements load on these factors and others.
Method of Factor Extraction
The first methodology choice for factor analysis is the mathematical approach for extracting the factors from your dataset. The most common choices are maximum likelihood (ML), principal axis factoring (PAF), and principal components analysis (PCA).
You should use either ML or PAF most of the time.
Use ML when your data follow a normal distribution. In addition to extracting factor loadings, it also can perform hypothesis tests, construct confidence intervals, and calculate goodness-of-fit statistics .
Use PAF when your data violates multivariate normality. PAF doesn’t assume that your data follow any distribution, so you could use it when they are normally distributed. However, this method can’t provide all the statistical measures as ML.
PCA is the default method for factor analysis in some statistical software packages, but it isn’t a factor extraction method. It is a data reduction technique to find components. There are technical differences, but in a nutshell, factor analysis aims to reveal latent factors while PCA is only for data reduction. While calculating the components, PCA doesn’t assess the underlying commonalities that unobserved factors cause.
PCA gained popularity because it was a faster algorithm during a time of slower, more expensive computers. If you’re using PCA for factor analysis, do some research to be sure it’s the correct method for your study. Learn more about PCA in, Principal Component Analysis Guide and Example .
There are other methods of factor extraction, but the factor analysis literature has not strongly shown that any of them are better than maximum likelihood or principal axis factoring.
Number of Factors to Extract
You need to specify the number of factors to extract from your data except when using principal component components. The method for determining that number depends on whether you’re performing exploratory or confirmatory factor analysis.
Exploratory Factor Analysis
In EFA, researchers must specify the number of factors to retain. The maximum number of factors you can extract equals the number of variables in your dataset. However, you typically want to reduce the number of factors as much as possible while maximizing the total amount of variance the factors explain.
That’s the notion of a parsimonious model in statistics. When adding factors, there are diminishing returns. At some point, you’ll find that an additional factor doesn’t substantially increase the explained variance. That’s when adding factors needlessly complicates the model. Go with the simplest model that explains most of the variance.
Fortunately, a simple statistical tool known as a scree plot helps you manage this tradeoff.
Use your statistical software to produce a scree plot. Then look for the bend in the data where the curve flattens. The number of points before the bend is often the correct number of factors to extract.
The scree plot below relates to the factor analysis example later in this post. The graph displays the Eigenvalues by the number of factors. Eigenvalues relate to the amount of explained variance.

The scree plot shows the bend in the curve occurring at factor 6. Consequently, we need to extract five factors. Those five explain most of the variance. Additional factors do not explain much more.
Some analysts and software use Eigenvalues > 1 to retain a factor. However, simulation studies have found that this tends to extract too many factors and that the scree plot method is better. (Costello & Osborne, 2005).
Of course, as you explore your data and evaluate the results, you can use theory and subject-area knowledge to adjust the number of factors. The factors and their interpretations must fit the context of your study.
Confirmatory Factor Analysis
In CFA, researchers specify the number of factors to retain using existing theory or measurement instruments before performing the analysis. For example, if a measurement instrument purports to assess three constructs, then the factor analysis should extract three factors and see if the results match theory.
Factor Loadings
In factor analysis, the loadings describe the relationships between the factors and the observed variables. By evaluating the factor loadings, you can understand the strength of the relationship between each variable and the factor. Additionally, you can identify the observed variables corresponding to a specific factor.
Interpret loadings like correlation coefficients . Values range from -1 to +1. The sign indicates the direction of the relations (positive or negative), while the absolute value indicates the strength. Stronger relationships have factor loadings closer to -1 and +1. Weaker relationships are close to zero.
Stronger relationships in the factor analysis context indicate that the factors explain much of the variance in the observed variables.
Related post : Correlation Coefficients
Factor Rotations
In factor analysis, the initial set of loadings is only one of an infinite number of possible solutions that describe the data equally. Unfortunately, the initial answer is frequently difficult to interpret because each factor can contain middling loadings for many indicators. That makes it hard to label them. You want to say that particular variables correlate strongly with a factor while most others do not correlate at all. A sharp contrast between high and low loadings makes that easier.
Rotating the factors addresses this problem by maximizing and minimizing the entire set of factor loadings. The goal is to produce a limited number of high loadings and many low loadings for each factor.
This combination lets you identify the relatively few indicators that strongly correlate with a factor and the larger number of variables that do not correlate with it. You can more easily determine what relates to a factor and what does not. This condition is what statisticians mean by simplifying factor analysis results and making them easier to interpret.
Graphical illustration
Let me show you how factor rotations work graphically using scatterplots .
Factor analysis starts by calculating the pattern of factor loadings. However, it picks an arbitrary set of axes by which to report them. Rotating the axes while leaving the data points unaltered keeps the original model and data pattern in place while producing more interpretable results.
To make this graphable in two dimensions, we’ll use two factors represented by the X and Y axes. On the scatterplot below, the six data points represent the observed variables, and the X and Y coordinates indicate their loadings for the two factors. Ideally, the dots fall right on an axis because that shows a high loading for that factor and a zero loading for the other.

For the initial factor analysis solution on the scatterplot, the points contain a mixture of both X and Y coordinates and aren’t close to a factor’s axis. That makes the results difficult to interpret because the variables have middling loads on all the factors. Visually, they’re not clumped near axes, making it difficult to assign the variables to one.
Rotating the axes around the scatterplot increases or decreases the X and Y values while retaining the original pattern of data points. At the blue rotation on the graph below, you maximize one factor loading while minimizing the other for all data points. The result is that the loads are high on one indicator but low on the other.

On the graph, all data points cluster close to one of the two factors on the blue rotated axes, making it easy to associate the observed variables with one factor.
Types of Rotations
Throughout these rotations, you work with the same data points and factor analysis model. The model fits the data for the rotated loadings equally as well as the initial loadings, but they’re easier to interpret. You’re using a different coordinate system to gain a different perspective of the same pattern of points.
There are two fundamental types of rotation in factor analysis, oblique and orthogonal.
Oblique rotations allow correlation amongst the factors, while orthogonal rotations assume they are entirely uncorrelated.
Graphically, orthogonal rotations enforce a 90° separation between axes, as shown in the example above, where the rotated axes form right angles.
Oblique rotations are not required to have axes forming right angles, as shown below for a different dataset.

Notice how the freedom for each axis to take any orientation allows them to fit the data more closely than when enforcing the 90° constraint. Consequently, oblique rotations can produce simpler structures than orthogonal rotations in some cases. However, these results can contain correlated factors.
| Promax | Varimax |
| Oblimin | Equimax |
| Direct Quartimin | Quartimax |
In practice, oblique rotations produce similar results as orthogonal rotations when the factors are uncorrelated in the real world. However, if you impose an orthogonal rotation on genuinely correlated factors, it can adversely affect the results. Despite the benefits of oblique rotations, analysts tend to use orthogonal rotations more frequently, which might be a mistake in some cases.
When choosing a rotation method in factor analysis, be sure it matches your underlying assumptions and subject-area knowledge about whether the factors are correlated.
Factor Analysis Example
Imagine that we are human resources researchers who want to understand the underlying factors for job candidates. We measured 12 variables and perform factor analysis to identify the latent factors. Download the CSV dataset: FactorAnalysis
The first step is to determine the number of factors to extract. Earlier in this post, I displayed the scree plot, which indicated we should extract five factors. If necessary, we can perform the analysis with a different number of factors later.
For the factor analysis, we’ll assume normality and use Maximum Likelihood to extract the factors. I’d prefer to use an oblique rotation, but my software only has orthogonal rotations. So, we’ll use Varimax. Let’s perform the analysis!
Interpreting the Results

In the bottom right of the output, we see that the five factors account for 81.8% of the variance. The %Var row along the bottom shows how much of the variance each explains. The five factors are roughly equal, explaining between 13.5% to 19% of the variance. Learn about Variance .
The Communality column displays the proportion of the variance the five factors explain for each variable. Values closer to 1 are better. The five factors explain the most variance for Resume (0.989) and the least for Appearance (0.643).
In the factor analysis output, the circled loadings show which variables have high loadings for each factor. As shown in the table below, we can assign labels encompassing the properties of the highly loading variables for each factor.
| 1 | Relevant Background | Academic record, Potential, Experience |
| 2 | Personal Characteristics | Confidence, Likeability, Appearance |
| 3 | General Work Skills | Organization, Communication |
| 4 | Writing Skills | Letter, Resume |
| 5 | Overall Fit | Company Fit, Job Fit |
In summary, these five factors explain a large proportion of the variance, and we can devise reasonable labels for each. These five latent factors drive the values of the 12 variables we measured.
Hervé Abdi (2003), “Factor Rotations in Factor Analyses,” In: Lewis-Beck M., Bryman, A., Futing T. (Eds.) (2003). Encyclopedia of Social Sciences Research Methods . Thousand Oaks (CA): Sage.
Brown, Michael W., (2001) “ An Overview of Analytic Rotation in Exploratory Factor Analysis ,” Multivariate Behavioral Research , 36 (1), 111-150.
Costello, Anna B. and Osborne, Jason (2005) “ Best practices in exploratory factor analysis: four recommendations for getting the most from your analysis ,” Practical Assessment, Research, and Evaluation : Vol. 10 , Article 7.
Share this:

Reader Interactions
September 29, 2024 at 10:44 am
I have been saving and referring to your posts for the past few years and as a beginner researcher, I find them invaluable. I have just started my PHD journey of developing and validating a mental health literacy measure for adolescents. Our approach is a mixed methods research design including a survey and Delphi panel with Item generation for the survey well on its way. I am totally out of my depth here and would be grateful for your input in terms of the way forward with regards to the analysis and integration of the quantitative and qualitative data.
Your guidance and insights would be deeply appreciated.
Kind regards Michelle
May 26, 2024 at 8:51 am
Good day Jim, I am running in troubles in terms of the item analysis on the 5 point Likert scale that I am trying to create. The thing is, is that my CFI is around 0.9 and TLI is around 0.8 which is good but my RMSEA and SRMR has a awful result as the RMSEA is around 0.1 and SRMR is 0.2. And it is a roadblock for me, I want to ask on how I can improve my RMSEA and SRMR? so that it would reach the cut off.
I hope that his message would reach you and thank you for taking the time and reading and responding to my troubled question.
May 15, 2024 at 11:27 am
Good day, Sir Jim. I am currently trying to create a 5-Likert scale that tries to measure National Identity Conformity in three ways: (1) Origin – (e.g., Americans are born in/from America), (2) Culture (e.g., Americans are patriotic) and (3) Belief (e.g., Americans embrace being Americans).
In the process of establishing the scale’s validity, I was told to use Exploratory Factor Analysis, and I would like to ask what methods of extraction and rotation can be best used to ensure that the inter-item validity of my scale is good. I would also like to understand how I can avoid crossloading or limit crossloading factors.
May 15, 2024 at 3:13 pm
I discuss those issues in this post. I’d recommend PAF as the method of extraction because your data being Likert scale won’t be normally distribution. Read the Method of Factor Extraction section for more information.
As for cross-loading, the method of rotation can help with that. The choice depends largely on subject-area knowledge and what works best for your data, so I can’t provide a suggested method. Read the Factor Rotations section for more information about that. For instance, if you get cross-loadings with orthogonal rotations, using an oblique rotation might help.
If factor rotation doesn’t sufficiently reduce cross-loading, you might need to rework your questions so they’re more distinct, remove problematic items, or increase your sample size (can provide more stable factor solutions and clearer patterns of loadings). In this scenario where changing rotations doesn’t help, you’ll need to determine whether the underlying issue is with your questions or having to small of a sample size.
I hope that helps!
March 6, 2024 at 10:20 pm
What does negative loadings mean? How to proceed further with these loadings?
March 6, 2024 at 10:44 pm
Loadings are like correlation coefficients and range from -1 to +1. More extreme positive and negative values indicate stronger relationships. Negative loadings indicate a negative relationship between the latent factors and observed variables. Highly negative values are as good as highly positive values. I discuss this in detail in the the Factor Loadings section of this post.
March 6, 2024 at 10:10 am
Good day Jim,
The methodology seems loaded with opportunities for errors. So often we are being asked to translate a nebulous English word into some sort of mathematical descriptor. As an example, in the section labelled ‘Interpreting the Results’, what are we to make of the words ‘likeability’ or ‘self-confidence’ ? How can we possibly evaluate those things…and to three significant decimal places ?
You Jim, understand and use statistical methods correctly. Yet, too often people who apply statistics fail to examine the language of their initial questions and end up doing poor analysis. Worse, many don’t understand the software they use.
On a more cheery note, keep up the great work. The world needs a thousand more of you.
March 6, 2024 at 5:08 pm
Thanks for the thoughtful comment. I agree with your concerns.
Ideally, all of those attributes are measured using validated measurement scales. The field of psychology is pretty good about that for terms that seem kind of squishy. For instance, they usually have thorough validation processes for personality traits, etc. However, your point is well taken, you need to be able to trust your data.
All statistical analyses depend on thorough subject-area knowledge, and that’s very true for factor analysis. You must have a solid theoretical understanding of these latent factors from extensive research before considering FA. Then FA can see if there’s evidence that they actually exist. But, I do agree with you that between the rotations and having to derive names to associate with the loadings, it can be a fairly subjective process.
Thanks so much for your kind words! I appreciate them because I do strive for accuracy.
March 2, 2024 at 8:44 pm
sir, i want to know that after successfully identifying my 3 factors with above give method now i want to regress on the data how to get single value for each factor rather than these number of values
February 28, 2024 at 7:48 am
Hello, Thanks for your effort on this post, it really helped me a lot. I want your recommendation for my case if you don’t mind.
I’m working on my research and I’ve 5 independent variables and 1 dependent variable, I want to use a factor analysis method in order to know which variable contributes the most in the dependent variable.
Also, what kind of data checks and preparations shall I make before starting the analysis.
Thanks in advance for your consideration.
February 28, 2024 at 1:46 pm
Based on the information you provided, I don’t believe factor analysis is the correct analysis for you.
Factor analysis is primarily used for understanding the structure of a set of variables and for reducing data dimensions by identifying underlying latent factors. It’s particularly useful when you have a large number of observed variables and believe that they are influenced by a smaller number of unobserved factors.
Instead, it sounds like you have the IVs and DV and want to understand the relationships between them. For that, I recommend multiple regression. Learn more in my post about When to Use Regression . After you settle on a model, there are several ways to Identify the Most Important Variables in the Model .
In terms of checking assumptions, familiarize yourself with the Ordinary Least Squares Regression Assumptions . Least squares regression is the most common and is a good place to start.
Best of luck with your analysis!
December 1, 2023 at 1:01 pm
What would be the eign value in efa
November 1, 2023 at 4:42 am
Hi Jim, this is an excellent yet succinct article on the topic. A very basic question, though: the dataset contains ordinal data. Is this ok? I’m a student in a Multivariate Statistics course, and as far as I’m aware, both PCA and common factor analysis dictate metric data. Or is it assumed that since the ordinal data has been coded into a range of 0-10, then the data is considered numeric and can be applied with PCA or CFA?
Sorry for the dumb question, and thank you.
November 1, 2023 at 8:00 pm
That’s a great question.
For the example in this post, we’re dealing with data on a 10 point scale where the differences between all points are equal. Consequently, we can treat discrete data as continuous data.
Now, to your question about ordinal data. You can use ordinal data with factor analysis however you might need to use specific methods.
For ordinal data, it’s often recommended to use polychoric correlations instead of Pearson correlations. Polychoric correlations estimate the correlation between two latent continuous variables that underlie the observed ordinal variables. This provides a more accurate correlation matrix for factor analysis of ordinal data.
I’ve also heard about categorical PCA and nonlinear Factor Analysis that use a monotonical transformation of ordinal data.
I hope that helps clarify it for you!
September 2, 2023 at 4:14 pm
Once identifying how much each variability the factors contribute, what steps could we take from here to make predictions about variables ?
September 2, 2023 at 6:53 pm
Hi Brittany,
Thanks for the great question! And thanks for you kind words in your other comment! 🙂
What you can do is calculate all the factor scores for each observation. Some software will do this for you as an option. Or, you can input values into the regression equations for the factor scores that are included in the output.
Then use these scores as the independent variables in regression analysis. From there, you can use the regression model to make predictions .
Ideally, you’d evaluate the regression model before making predictions and use cross validation to be sure that the model works for observations outside the dataset you used to fit the model.
September 2, 2023 at 4:13 pm
Wow! This was really helpful and structured very well for interpretation. Thank you!
October 6, 2022 at 10:55 am
I can imagine that Prof will have further explanations on this down the line at some point in future. I’m waiting… Thanks Prof Jim for your usual intuitive manner of explaining concepts. Funsho
September 26, 2022 at 8:08 am
Thanks for a very comprehensive guide. I learnt a lot. In PCA, we usually extract the components and use it for predictive modeling. Is this the case with Factor Analysis as well? Can we use factors as predictors?
September 26, 2022 at 8:27 pm
I have not used factors as predictors, but I think it would be possible. However, PCA’s goal is to maximize data reduction. This process is particularly valuable when you have many variables, low sample size and/or collinearity between the predictors. Factor Analysis also reduces the data but that’s not its primary goal. Consequently, my sense is that PCA is better for that predictive modeling while Factor Analysis is better for when you’re trying to understand the underlying factors (which you aren’t with PCA). But, again, I haven’t tried using factors in that way nor I have compared the results to PCA. So, take that with a grain of salt!
Comments and Questions Cancel reply

- > Machine Learning
Factor Analysis: Types & Applications
- Soumyaa Rawat
- Sep 14, 2021

What is Factor Analysis ?
Data is everywhere. From data research to artificial intelligence technology, data has become an essential commodity that is being perceived as a link between our past and future. Is an organization willing to collect its past records?
Data is the key solution to this problem. Is any programmer willing to formulate a Machine Learning algorithm ? Data is what s/he needs to begin with.
While the world has moved on to technology, it still is unaware of the fact that data is the building block of all these technological advancements that have together made the world so advanced.
When it comes to data, a number of tools and techniques are put to work to arrange, organize, and accumulate data the way one wants to. Factor Analysis is one of them. A data reduction technique, Factor Analysis is a statistical method used to reduce the number of observed factors for a much better insight into a given dataset.
But first, we shall understand what is a factor. A factor is a set of observed variables that have similar responses to an action. Since variables in a given dataset can be too much to deal with, Factor Analysis condenses these factors or variables into fewer variables that are actionable and substantial to work upon.
A technique of dimensionality reduction in data mining, Factor Analysis works on narrowing the availability of variables in a given data set, allowing deeper insights and better visibility of patterns for data research.
Most commonly used to identify the relationship between various variables in statistics , Factor Analysis can be thought of as a compressor that compresses the size of variables and produces a much enhanced, insightful, and accurate variable set.
“FA is considered an extension of principal component analysis since the ultimate objective for both techniques is a data reduction.” Factor Analysis in Data Reduction
Types of Factor Analysis
Developed in 1904 by Spearman, Factor Analysis is broadly divided into various types based upon the approach to detect underlying variables and establish a relationship between them.
While there are a variety of techniques to conduct factor analysis like Principal Component Analysis or Independent Component Analysis , Factor Analysis can be divided into 2 types which we will discuss below. Let us get started.
Confirmatory Factor Analysis
As the name of this concept suggests, Confirmatory Factor Analysis (CFA) lets one determine whether a relationship between factors or a set of overserved variables and their underlying components exists.
It helps one confirm whether there is a connection between two components of variables in a given dataset. Usually, the purpose of CFA is to test whether certain data fit the requirements of a particular hypothesis.
The process begins with a researcher formulating a hypothesis that is made to fit along the lines of a certain theory. If the constraints imposed on a model do not fit well with the data, then the model is rejected, and it is confirmed that no relationship exists between a factor and its underlying construct. Perhaps hypothetical testing also finds a space in the world of Factor Analysis.
Exploratory Factor Analysis
In the case of Exploratory Factor Statistical Analysis , the purpose is to determine/explore the underlying latent structure of a large set of variables. EFA, unlike CFA, tends to uncover the relationship, if any, between measured variables of an entity (for example - height, weight, etc. in a human figure).
While CFA works on finding a relationship between a set of observed variables and their underlying structure, this works to uncover a relationship between various variables within a given dataset.
Conducting Exploratory Factor Analysis involves figuring the total number of factors involved in a dataset.
“EFA is generally considered to be more of a theory-generating procedure than a theory-testing procedure. In contrast, confirmatory factor analysis (CFA) is generally based on a strong theoretical and/or empirical foundation that allows the researcher to specify an exact factor model in advance.” EFA in Hypothesis Testing
Applications of Factor Analysis
With immense use in various fields in real life, this segment presents a list of applications of Factor Analysis and the way FA is used in day-to-day operations.
Applications of factor analysis
Marketing is defined as the act of promoting a good or a service or even a brand. When it comes to Factor Analysis in marketing, one can benefit immensely from this statistical method.
In order to boost marketing campaigns and accelerate success, in the long run, companies employ Factor Analysis techniques that help to find a correlation between various variables or factors of a marketing campaign.
Moreover, FA also helps to establish connections with customer satisfaction and consequent feedback after a marketing campaign in order to check its efficacy and impact on the audiences.
That said, the realm of marketing can largely benefit from Factor Analysis and trigger sales with respect to much-enhanced feedback and customer satisfaction reports.
(Must read: Marketing management guide )
Data Mining
In data mining, Factor Analysis can play a role as important as that of artificial intelligence. Owing to its ability to transform a complex and vast dataset into a group of filtered out variables that are related to each other in some way or the other, FA eases out the process of data mining.
For data scientists, the tedious task of finding relationships and establishing correlation among various variables has always been full of obstacles and errors.
However, with the help of this statistical method, data mining has become much more advanced.
(Also read: Data mining tools )
Machine Learning
Machine Learning and data mining tools go hand in hand. Perhaps this is the reason why Factor Analysis finds a place among Machine Learning tools and techniques.
As Factor Analysis in machine learning helps in reducing the number of variables in a given dataset to procure a more accurate and enhanced set of observed factors, various machine learning algorithms are put to use to work accordingly.
They are trained well with humongous data to rightly work in order to give way to other applications. An unsupervised machine learning algorithm, FA is largely used for dimensionality reduction in machine learning.
Thereby, machine learning can very well collaborate with Factor Analysis to give rise to data mining techniques and make the task of data research massively efficient.
(Recommended blog: Data mining software )
Nutritional Science
Nutritional Science is a prominent field of work in the contemporary scenario. By focusing on the dietary practices of a given population, Factor Analysis helps to establish a relationship between the consumption of nutrients in an adult’s diet and the nutritional health of that person.
Furthermore, an individual’s nutrient intake and consequent health status have helped nutritionists to compute the appropriate quantity of nutrients one should intake in a given period of time.
The application of Factor Analysis in business is rather surprising and satisfactory.
Remember the times when business firms had to employ professionals to dig out patterns from past records in order to lay a road ahead for strategic business plans?
Well, gone are the days when so much work had to be done. Thanks to Factor Analysis, the world of business can use it for eliminating the guesswork and formulating more accurate and straightforward decisions in various aspects like budgeting, marketing, production, and transport.
Pros and Cons of Factor Analysis
Having learned about Factor Analysis in detail, let us now move on to looking closely into the pros and cons of this statistical method.
Pros of Factor Analysis
Measurable attributes.
The first and foremost pro of FA is that it is open to all measurable attributes. Be it subjective or objective, any kind of attribute can be worked upon when it comes to this statistical technique.
Unlike some statistical models that only work on objective attributes, Factor Analysis goes well with both subjective and objective attributes.
Cost-Effective
While data research and data mining algorithms can cost a lot due to the extraordinary charges, this statistical model is surprisingly cost-effective and does not take many resources to work with.
That said, it can be incorporated by any beginner or an experienced professional in light of its cost-effective and easy approach towards data mining and data reduction.
Flexible Approach
While many machine learning algorithms are rigid and constricted to a single approach, Factor Analysis does not work that way.
Rather, this statistical model has a flexible approach towards multivariate datasets that let one obtain relationships or correlations between various variables and their underlying components.
(Must read: AI algorithms )
Cons of Factor Analysis
Incomprehensive results.
While there are many pros of Factor Analysis, there are various cons of this method as well. Primarily, Factor Analysis can procure incompetent results due to incomprehensive datasets.
While various data points can have similar traits, some other variables or factors can go unnoticed due to being isolated in a vast dataset. That said, the results of this method could be incomprehensive.
Non-Identification of Complicated Factors
Another drawback of Factor Analysis is that it does not identify complicated factors that underlie a dataset.
While some results could clearly indicate a correlation between two variables, some complicated correlations can go unnoticed in such a method.
Perhaps the non-identification of complicated factors and their relationships could be an issue for data research.
Reliant on Theory
Even though Factor Analysis skills can be imitated by machine learning algorithms, this method is still reliant on theory and thereby data researchers.
While many components of a dataset can be handled by a computer, some other details are required to be looked into by humans.
Thus, one of the major drawbacks of Factor Analysis is that it is somehow reliant on theory and cannot fully function without manual assistance.
(Suggested reading: Deep learning algorithms )
Summing Up
To sum up, Factor Analysis is an extensive statistical model that is used to reduce dimensions of a given dataset with the help of condensing observed variables in a smaller size.
(Top reading: Statistical data distribution models )
By arranging observed variables in groups of super-variables, Factor Analysis has immensely impacted the way data mining is done. With numerous fields relying on this technique for better performance, FA is the need of the hour.
Share Blog :
Be a part of our Instagram community
Trending blogs
5 Factors Influencing Consumer Behavior
Elasticity of Demand and its Types
An Overview of Descriptive Analysis
What is PESTLE Analysis? Everything you need to know about it
What is Managerial Economics? Definition, Types, Nature, Principles, and Scope
5 Factors Affecting the Price Elasticity of Demand (PED)
6 Major Branches of Artificial Intelligence (AI)
Scope of Managerial Economics
Dijkstra’s Algorithm: The Shortest Path Algorithm
Different Types of Research Methods
Latest Comments

Contact Us (315) 303-2040
- Market Research Company Blog
Factor Analysis In Research: Types & Examples
by Tim Gell
Posted at: 7/1/2024 12:30 PM

Factor analysis in market research is a statistical method used to uncover underlying dimensions, or factors, in a dataset.
By examining patterns of correlation between variables, factor analysis helps to identify groups of variables that are highly interrelated and can be used to explain a common underlying theme.
Factor analysis can be best used for complex situations where there are many data sets and potentially many variables to summarize.
In this blog, we will explore the different types of factor analysis, their benefits, and examples of when to use them.
What is Factor Analysis?
Factor analysis is a commonly used data reduction statistical technique within the context of market research. The goal of factor analysis is to discover relationships between variables within a dataset by looking at correlations.
This advanced technique groups questions that are answered similarly among respondents in a survey.
The output will be a set of latent factors that represent questions that “move” together.
In other words, a resulting factor may consist of several survey questions whose data tend to increase or decrease in unison.
If you don’t need the underlying factors in your dataset and just want to understand the relationship between variables, regression analysis may be a better fit.
Things to Remember for Factor Analysis
There are a few concepts to keep in mind when doing factor analysis. These concepts guide the way that factor analysis is applied to certain projects and it’s interpretation.
- Variance: This measures how much values are off from the average. Since you want to understand the influence of the factors, variance will help understand how much variance there is in the results.
- Factor Score: This is a number representation of how strong each variable is from the original data. This is also related to a specific factor and can also be called the “component score”. It helps determine which variables are most changed by factors and which are most important.
- Factor Loading: this is typically a coefficient for correlation related to the variable/factor combination. Higher factor loadings means there is a stronger influence on the variables.
What are the Different Types of Factor Analysis?
When discussing this topic, it is always good to distinguish between the different types of factor analysis.
There are different approaches that achieve similar results in the end, but it's important to understand that there is different math going on behind the scenes for each method.
Types of factor analysis include:
- Principal component analysis
- Exploratory factor analysis
- Confirmatory factor analysis
1. Principal component analysis
Factor analysis assumes the existence of latent factors within the dataset, and then works backward from there to identify the factors.
In contrast, principal component analysis (also known as PCA) uses the variables within a dataset to create a composite of the other variables.
With PCA, you're starting with the variables and then creating a weighted average called a “component,” similar to a factor.
2. Exploratory factor analysis
In exploratory factor analysis, you're forming a hypothesis about potential relationships between your variables.
You might be using this approach if you're not sure what to expect in the way of factors.
You may need assistance with identifying the underlying themes among your survey questions and in this case, I recommend working with a market research company , like Drive Research.
Exploratory factor analysis ultimately helps understand how many factors are present in the data and what the skeleton of the factors might look like.
The process involves a manual review of factor loadings values for each data input, which are outputs to assess the suitability of the factors.
Do these factors make sense? If they don’t make adjustments to the inputs and try again.
If they do, you often move forward to the next step of confirmatory factor analysis.
3. Confirmatory factor analysis
Exploratory factor analysis and confirmatory factor analysis go hand in hand.
Now that you have a hypothesis from exploratory factor analysis, confirmatory factor analysis is going to test that hypothesis of potential relationships in your variables.
This process is essentially fine-tuning your factors so that you land at a spot where the factors make sense with respect to your objectives.
The sought outcome of confirmatory factor analysis is to achieve statistically sound and digestible factors for yourself or a client.
A best practice for confirmatory factor analysis is testing the model's goodness of fit.
This involves splitting your data into two equal segments: a test set and a training set.
The next step is to test the goodness of fit on that training data set, which includes applying the created factors from the training data set to the test dataset.
If you achieve similar factors in both sets, this then gives you thumbs up that the model is statistically valid.
How Factor Analysis Can Benefit You
1. Spot trends within your data
If you are part of a business and leveraging factor analysis with your data, some of the advantages include the ability to spot trends or themes within your data.
Certain attributes may be connected in a way you wouldn’t have known otherwise.
You may learn that different customer behaviors and attitudes are closely related. This knowledge can be used to inform marketing decisions when it comes to your product or service.
2. Pinpoint the number of factors in a data set
Factor analysis, or exploratory factor analysis more specifically, can also be used to pinpoint the right number of factors within a data set.
Knowing how many overarching factors you need to worry about allows you to spend your time focusing on the aspects of your data that have the greatest impact.
This will save you time, instill confidence in the results, and equip you with more actionable information.
3. Streamlines segmenting data
Lastly, factor analysis can be a great first step and lead-in for a cluster analysis if you are planning a customer segmentation study .
As a prerequisite, factor analysis streamlines the inputs for your segmentation. It helps to eliminate redundancies or irrelevant data, giving you a result that is clearer and easier to understand.
Here are 6 easy steps to conducting customer segmentation . Factor analysis could fit nicely between Step 3 and Step 4 if you are working with a high number of inputs.
When We Recommend Using Factor Analysis
Factor analysis is a great tool when working with large sets of interconnected data.
In our experience, it’s designed to help companies understand the hidden patterns or structures within data collected. It can simplify complex information, which is especially important when managing numerous variables.
For example, if your company gathered extensive customer feedback through surveys, factor analysis can transform those responses into more manageable, meaningful categories.
Factor analysis helps condense variables like customer satisfaction, product quality, and customer service into broader factors like 'product satisfaction' or 'customer experience'.
Examples of Performing a Factor Analysis
With so many types of market research , factor analysis has a wide range of applications.
Although, employee surveys and customer surveys are two of the best examples of when factor analysis is most helpful.
1. Employee surveys
For example, when using a third party for employee surveys, ask if the employee survey company can use factor analysis.
In these surveys, businesses aim to learn what matters most to their employees.
Because there is a myriad of variables that impact the employee experience, factor analysis has the potential to narrow down all these variables into a few manageable latent factors.
You might learn that flexibility, growth opportunities, and compensation are three key factors propelling your employees’ experiences.
Understanding these categories will make the management or hiring process that much easier.
2. Customer surveys
Factor analysis can also be a great application when conducting customer satisfaction surveys .
Let's say you have a lot of distinct variables going on in relation to customer preferences.
Customers are weighing these various product attributes each time before they make a purchase.
Factor analysis can group these attributes into useful factors, enabling you to see the forest through the trees.
You may have a hunch about what the categories would be, but factor analysis gives an approach backed by statistics to say this is how your product attributes should be grouped.
Factor Analysis Best Practices
1. Use the right inputs
For any market research study in which you plan to use factor analysis, you also need to make sure you have the proper inputs.
What it comes down to is asking survey questions that capture ordinal quantitative data.
Open-ended answers are not going to be useful for factor analysis.
Valid input data could involve rating scales, Likert scales, or even Yes/No questions that can be boiled down to binary ones and zeros.
Any combination of these questions could be effectively used for factor analysis.
2. Include enough data points
It is also imperative to include enough data inputs.
Running factor analysis on 50 attributes will tell you a whole lot more than an analysis on 5 attributes.
After all, the idea is to throw an unorganized mass of attributes into the analysis to see what latent factors really exist among them.
3. Large sample sizes are best
A large sample size will also convey more confidence when you share the results of the factor analysis.
At least 100 responses per audience segment in the analysis is a good starting point, if possible.
Contact Drive Research to Perform Factor Analysis
Drive Research is a national market research company that can help with lots of market research projects. Advanced methods like factor analysis are a part of our wheelhouse to get the most out of your data.
Interested in learning more about our market research services ? Reach out through any of the four ways below.
- Message us on our website
- Email us at [email protected]
- Call us at 888-725-DATA
- Text us at 315-303-2040

As a Senior Research Analyst, Tim is involved in every stage of a market research project for our clients. He first developed an interest in market research while studying at Binghamton University based on its marriage of business, statistics, and psychology
Learn more about Tim, here .

Categories: Market Research Analysis
Need help with your project? Get in touch with Drive Research.
View Our Blog
Root out friction in every digital experience, super-charge conversion rates, and optimise digital self-service
Uncover insights from any interaction, deliver AI-powered agent coaching, and reduce cost to serve
Increase revenue and loyalty with real-time insights and recommendations delivered straight to teams on the ground
Know how your people feel and empower managers to improve employee engagement, productivity, and retention
Take action in the moments that matter most along the employee journey and drive bottom line growth
Whatever they’re saying, wherever they’re saying it, know exactly what’s going on with your people
Get faster, richer insights with qual and quant tools that make powerful market research available to everyone
Run concept tests, pricing studies, prototyping + more with fast, powerful studies designed by UX research experts
Track your brand performance 24/7 and act quickly to respond to opportunities and challenges in your market
Meet the operating system for experience management
- Free Account
- Product Demos
- For Digital
- For Customer Care
- For Human Resources
- For Researchers
- Financial Services
- All Industries
Popular Use Cases
- Customer Experience
- Employee Experience
- Employee Exit Interviews
- Net Promoter Score
- Voice of Customer
- Customer Success Hub
- Product Documentation
- Training & Certification
- XM Institute
- Popular Resources
- Customer Stories
- Artificial Intelligence
- Market Research
- Partnerships
- Marketplace
The annual gathering of the experience leaders at the world’s iconic brands building breakthrough business results.
- English/AU & NZ
- Español/Europa
- Español/América Latina
- Português Brasileiro
- REQUEST DEMO
- Experience Management
- Survey Analysis
- Factor Analysis
Try Qualtrics for free
What is factor analysis and how does it simplify research findings.
17 min read There are many forms of data analysis used to report on and study survey data. Factor analysis is best when used to simplify complex data sets with many variables.
What is factor analysis?
Factor analysis is the practice of condensing many variables into just a few, so that your research data is easier to work with.
For example, a retail business trying to understand customer buying behaviours might consider variables such as ‘did the product meet your expectations?’, ‘how would you rate the value for money?’ and ‘did you find the product easily?’. Factor analysis can help condense these variables into a single factor, such as ‘customer purchase satisfaction’.
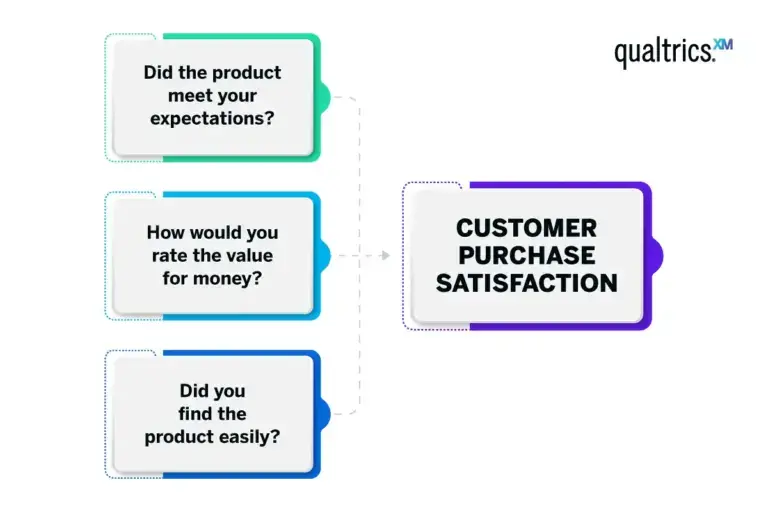
The theory is that there are deeper factors driving the underlying concepts in your data, and that you can uncover and work with them instead of dealing with the lower-level variables that cascade from them. Know that these deeper concepts aren’t necessarily immediately obvious – they might represent traits or tendencies that are hard to measure, such as extraversion or IQ.
Factor analysis is also sometimes called “dimension reduction”: you can reduce the “dimensions” of your data into one or more “super-variables,” also known as unobserved variables or latent variables. This process involves creating a factor model and often yields a factor matrix that organises the relationship between observed variables and the factors they’re associated with.
As with any kind of process that simplifies complexity, there is a trade-off between the accuracy of the data and how easy it is to work with. With factor analysis, the best solution is the one that yields a simplification that represents the true nature of your data, with minimum loss of precision. This often means finding a balance between achieving the variance explained by the model and using fewer factors to keep the model simple.
Factor analysis isn’t a single technique, but a family of statistical methods that can be used to identify the latent factors driving observable variables. Factor analysis is commonly used in market research , as well as other disciplines like technology, medicine, sociology, field biology, education, psychology and many more.
What is a factor?
In the context of factor analysis, a factor is a hidden or underlying variable that we infer from a set of directly measurable variables.
Take ‘customer purchase satisfaction’ as an example again. This isn’t a variable you can directly ask a customer to rate, but it can be determined from the responses to correlated questions like ‘did the product meet your expectations?’, ‘how would you rate the value for money?’ and ‘did you find the product easily?’.
While not directly observable, factors are essential for providing a clearer, more streamlined understanding of data. They enable us to capture the essence of our data’s complexity, making it simpler and more manageable to work with, and without losing lots of information.
Free eBook: 2024 global market research trends report
Key concepts in factor analysis
These concepts are the foundational pillars that guide the application and interpretation of factor analysis.
Central to factor analysis, variance measures how much numerical values differ from the average. In factor analysis, you’re essentially trying to understand how underlying factors influence this variance among your variables. Some factors will explain more variance than others, meaning they more accurately represent the variables they consist of.
The eigenvalue expresses the amount of variance a factor explains. If a factor solution (unobserved or latent variables) has an eigenvalue of 1 or above, it indicates that a factor explains more variance than a single observed variable, which can be useful in reducing the number of variables in your analysis. Factors with eigenvalues less than 1 account for less variability than a single variable and are generally not included in the analysis.
Factor score
A factor score is a numeric representation that tells us how strongly each variable from the original data is related to a specific factor. Also called the component score, it can help determine which variables are most influenced by each factor and are most important for each underlying concept.
Factor loading
Factor loading is the correlation coefficient for the variable and factor. Like the factor score, factor loadings give an indication of how much of the variance in an observed variable can be explained by the factor. High factor loadings (close to 1 or -1) mean the factor strongly influences the variable.
When to use factor analysis
Factor analysis is a powerful tool when you want to simplify complex data, find hidden patterns, and set the stage for deeper, more focused analysis.
It’s typically used when you’re dealing with a large number of interconnected variables, and you want to understand the underlying structure or patterns within this data. It’s particularly useful when you suspect that these observed variables could be influenced by some hidden factors.
For example, consider a business that has collected extensive customer feedback through surveys . The survey covers a wide range of questions about product quality, pricing, customer service and more. This huge volume of data can be overwhelming, and this is where factor analysis comes in. It can help condense these numerous variables into a few meaningful factors, such as ‘product satisfaction’, ‘customer service experience’ and ‘value for money’.
Factor analysis doesn’t operate in isolation – it’s often used as a stepping stone for further analysis. For example, once you’ve identified key factors through factor analysis, you might then proceed to a cluster analysis – a method that groups your customers based on their responses to these factors. The result is a clearer understanding of different customer segments, which can then guide targeted marketing and product development strategies.
By combining factor analysis with other methodologies, you can not only make sense of your data but also gain valuable insights to drive your business decisions.
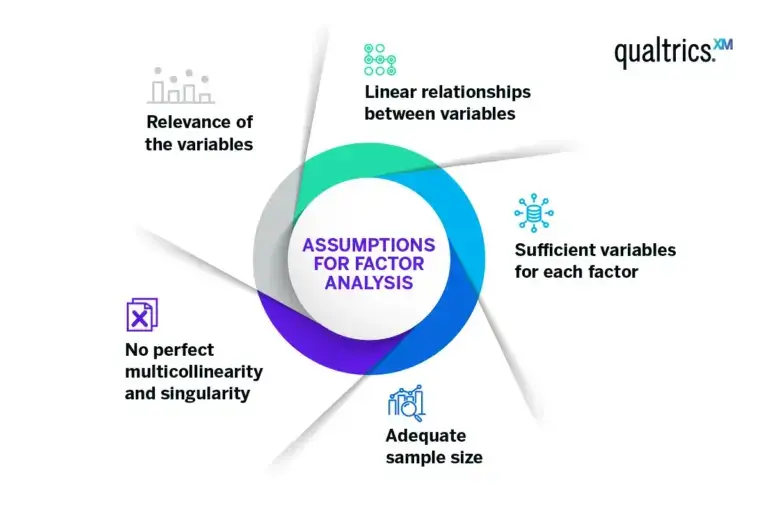
Factor analysis assumptions
Factor analysis relies on several assumptions for accurate results. Violating these assumptions may lead to factors that are hard to interpret or misleading.
Linear relationships between variables
This ensures that changes in the values of your variables are consistent.
Sufficient variables for each factor
Because if only a few variables represent a factor, it might not be identified accurately.
Adequate sample size
The larger the ratio of cases (respondents, for instance) to variables, the more reliable the analysis.
No perfect multicollinearity and singularity
No variable is a perfect linear combination of other variables, and no variable is a duplicate of another.
Relevance of the variables
There should be some correlation between variables to make a factor analysis feasible.
Types of factor analysis
There are two main factor analysis methods: exploratory and confirmatory. Here’s how they are used to add value to your research process.
Confirmatory factor analysis
In this type of analysis, the researcher starts out with a hypothesis about their data that they are looking to prove or disprove. Factor analysis will confirm – or not – where the latent variables are and how much variance they account for.
Principal component analysis (PCA) is a popular form of confirmatory factor analysis. Using this method, the researcher will run the analysis to obtain multiple possible solutions that split their data among a number of factors. Items that load onto a single particular factor are more strongly related to one another and can be grouped together by the researcher using their conceptual knowledge or pre-existing research.
Using PCA will generate a range of solutions with different numbers of factors, from simplified 1-factor solutions to higher levels of complexity. However, the fewer number of factors employed, the less variance will be accounted for in the solution.
Exploratory factor analysis
As the name suggests, exploratory factor analysis is undertaken without a hypothesis in mind. It’s an investigatory process that helps researchers understand whether associations exist between the initial variables, and if so, where they lie and how they are grouped.
How to perform factor analysis: A step-by-step guide
Performing a factor analysis involves a series of steps, often facilitated by statistical software packages like SPSS, Stata and the R programming language . Here’s a simplified overview of the process.
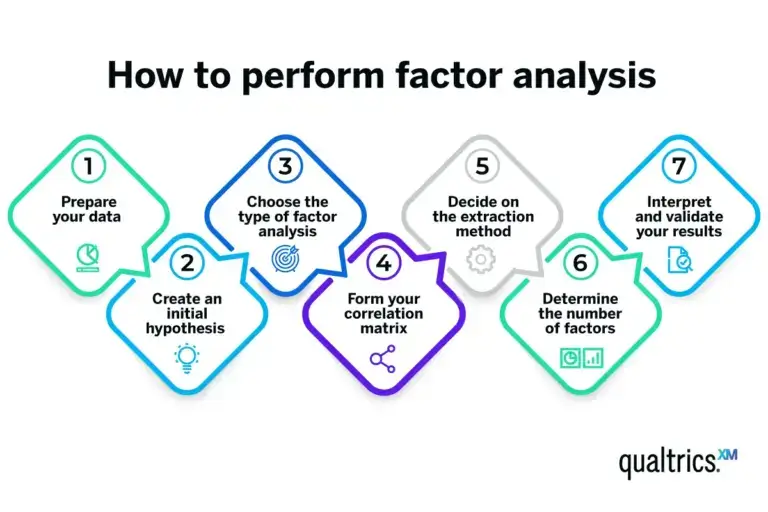
Prepare your data
Start with a dataset where each row represents a case (for example, a survey respondent), and each column is a variable you’re interested in. Ensure your data meets the assumptions necessary for factor analysis.
Create an initial hypothesis
If you have a theory about the underlying factors and their relationships with your variables, make a note of this. This hypothesis can guide your analysis, but keep in mind that the beauty of factor analysis is its ability to uncover unexpected relationships.
Choose the type of factor analysis
The most common type is exploratory factor analysis, which is used when you’re not sure what to expect. If you have a specific hypothesis about the factors, you might use confirmatory factor analysis.
Form your correlation matrix
After you’ve chosen the type of factor analysis, you’ll need to create the correlation matrix of your variables. This matrix, which shows the correlation coefficients between each pair of variables, forms the basis for the extraction of factors. This is a key step in building your factor analysis model.
Decide on the extraction method
Principal component analysis is the most commonly used extraction method. If you believe your factors are correlated, you might opt for principal axis factoring, a type of factor analysis that identifies factors based on shared variance.
Determine the number of factors
Various criteria can be used here, such as Kaiser’s criterion (eigenvalues greater than 1), the scree plot method or parallel analysis. The choice depends on your data and your goals.
Interpret and validate your results
Each factor will be associated with a set of your original variables, so label each factor based on how you interpret these associations. These labels should represent the underlying concept that ties the associated variables together.
Validation can be done through a variety of methods, like splitting your data in half and checking if both halves produce the same factors.
How factor analysis can help you
As well as giving you fewer variables to navigate, factor analysis can help you understand grouping and clustering in your input variables, since they’ll be grouped according to the latent variables.
Say you ask several questions all designed to explore different, but closely related, aspects of customer satisfaction:
- How satisfied are you with our product?
- Would you recommend our product to a friend or family member?
- How likely are you to purchase our product in the future?
But you only want one variable to represent a customer satisfaction score. One option would be to average the three question responses. Another option would be to create a factor dependent variable. This can be done by running a principal component analysis (PCA) and keeping the first principal component (also known as a factor). The advantage of a PCA over an average is that it automatically weights each of the variables in the calculation.
Say you have a list of questions and you don’t know exactly which responses will move together and which will move differently; for example, purchase barriers of potential customers. The following are possible barriers to purchase:
- Price is prohibitive
- Overall implementation costs
- We can’t reach a consensus in our organisation
- Product is not consistent with our business strategy
- I need to develop an ROI, but cannot or have not
- We are locked into a contract with another product
- The product benefits don’t outweigh the cost
- We have no reason to switch
- Our IT department cannot support your product
- We do not have sufficient technical resources
- Your product does not have a feature we require
- Other (please specify)
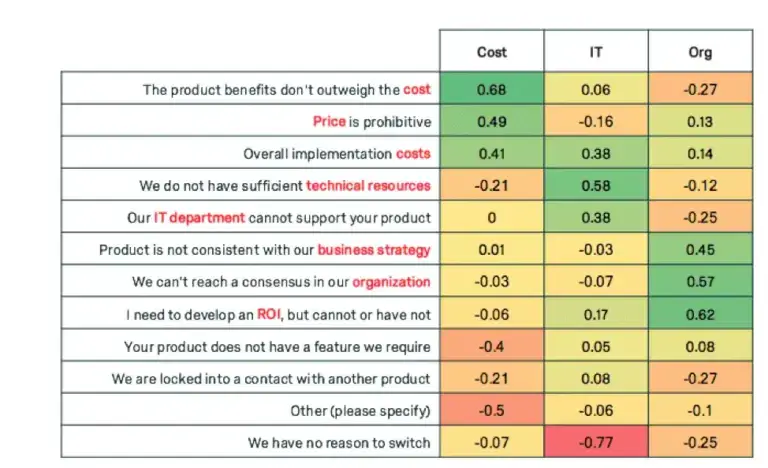
Factor analysis can uncover the trends of how these questions will move together. The following are loadings for 3 factors for each of the variables.
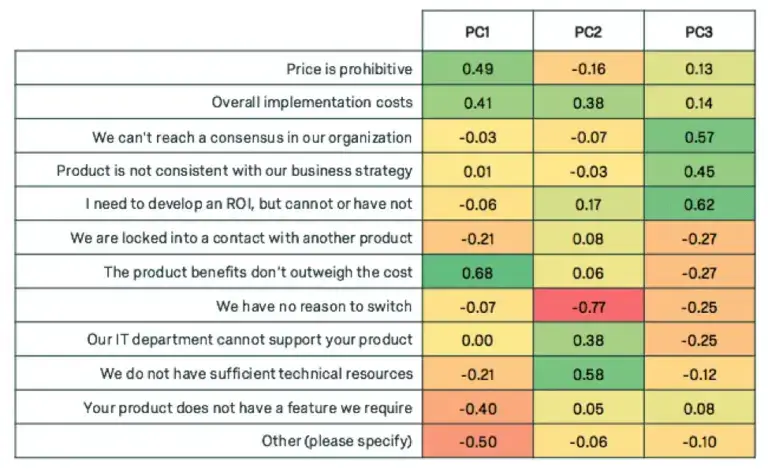
Notice how each of the principal components have high weights for a subset of the variables. Weight is used interchangeably with loading, and high weight indicates the variables that are most influential for each principal component. +0.30 is generally considered to be a heavy weight.
The first component displays heavy weights for variables related to cost, the second weights variables related to IT, and the third weights variables related to organisational factors. We can give our new super variables clever names.
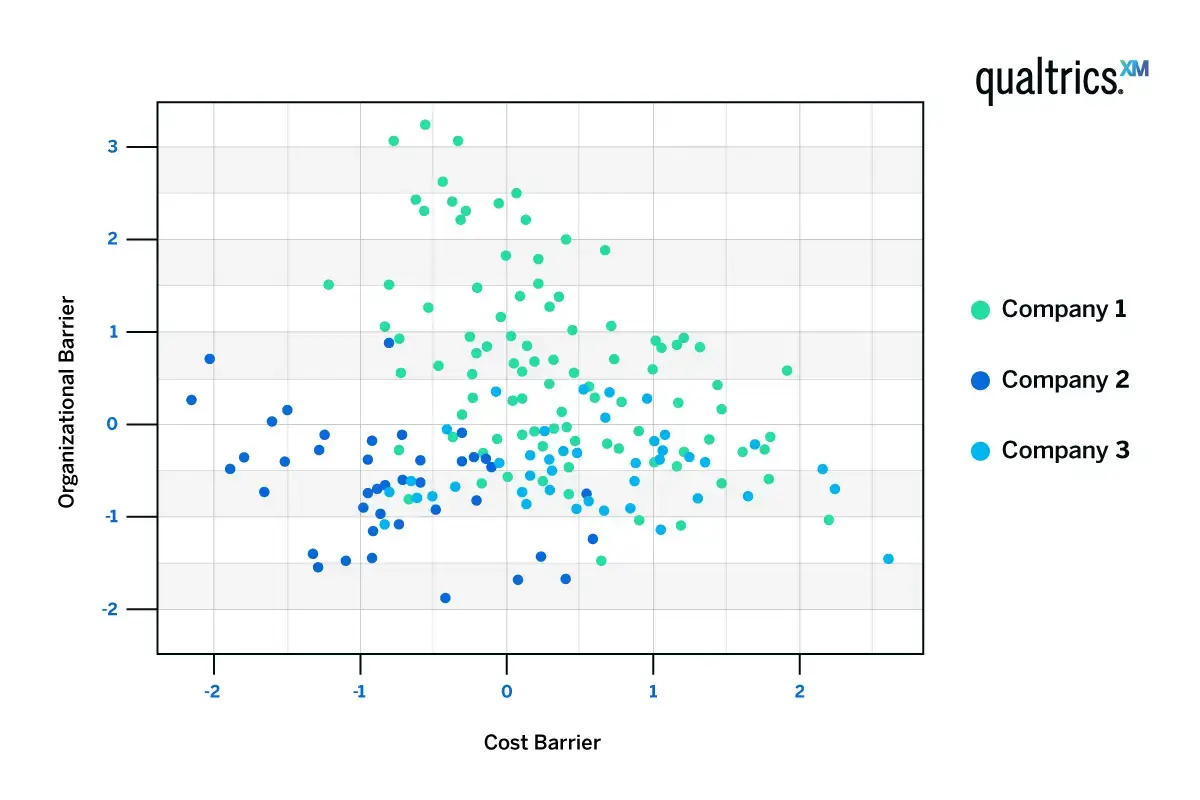
If we were to cluster the customers based on these three components, we can see some trends. Customers tend to be high in cost barriers or organisational barriers, but not both.
The red dots represent respondents who indicated they had higher organisational barriers; the green dots represent respondents who indicated they had higher cost barriers
Considerations when using factor analysis
Factor analysis is a tool, and like any tool its effectiveness depends on how you use it. When employing factor analysis, it’s essential to keep a few key considerations in mind.
Oversimplification
While factor analysis is great for simplifying complex data sets, there’s a risk of oversimplification when grouping variables into factors. To avoid this you should ensure the reduced factors still accurately represent the complexities of your variables.
Subjectivity
Interpreting the factors can sometimes be subjective, and requires a good understanding of the variables and the context. Be mindful that multiple analysts may come up with different names for the same factor.
Supplementary techniques
Factor analysis is often just the first step. Consider how it fits into your broader research strategy and which other techniques you’ll use alongside it.
Examples of factor analysis studies
Factor analysis, including PCA, is often used in tandem with segmentation studies . It might be an intermediary step to reduce variables before using KMeans to make the segments.
Factor analysis provides simplicity after reducing variables. For long studies with large blocks of Matrix Likert scale questions, the number of variables can become unwieldy. Simplifying the data using factor analysis helps analysts focus and clarify the results, while also reducing the number of dimensions they’re clustering on.
Sample questions for factor analysis
Choosing exactly which questions to perform factor analysis on is both an art and a science. Choosing which variables to reduce takes some experimentation, patience and creativity. Factor analysis works well on Likert scale questions and Sum to 100 question types.
Factor analysis works well on matrix blocks of the following question genres:
Psychographics (Agree/Disagree):
- I value family
- I believe brand represents value
Behavioural (Agree/Disagree):
- I purchase the cheapest option
- I am a bargain shopper
Attitudinal (Agree/Disagree):
- The economy is not improving
- I am pleased with the product
Activity-Based (Agree/Disagree):
- I love sports
- I sometimes shop online during work hours
Behavioural and psychographic questions are especially suited for factor analysis.
Sample output reports
Factor analysis simply produces weights (called loadings) for each respondent. These loadings can be used like other responses in the survey.
| Cost Barrier | IT Barrier | Org Barrier | |
|---|---|---|---|
| R_3NWlKlhmlRM0Lgb | 0.7 | 1.3 | -0.9 |
| R_Wp7FZE1ziZ9czSN | 0.2 | -0.4 | -0.3 |
| R_SJlfo8Lpb6XTHGh | -0.1 | 0.1 | 0.4 |
| R_1Kegjs7Q3AL49wO | -0.1 | -0.3 | -0.2 |
| R_1IY1urS9bmfIpbW | 1.6 | 0.3 | -0.3 |
Related resources
Analysis & Reporting
Margin of Error 11 min read
Text analysis 44 min read, sentiment analysis 21 min read, behavioural analytics 12 min read, descriptive statistics 15 min read, statistical significance calculator 18 min read, zero-party data 12 min read, request demo.
Ready to learn more about Qualtrics?
- Data Center
- Applications
- Open Source

Datamation content and product recommendations are editorially independent. We may make money when you click on links to our partners. Learn More .
Factor analysis is a powerful statistical technique used by data professionals in various business domains to uncover underlying data structures or latent variables. Factor analysis is sometimes confused with Fact Analysis of Information Risk, or FAIR, but they are not the same—factor analysis encompasses statistical methods for data reduction and identifying underlying patterns in various fields, while FAIR is a specific framework and methodology used for analyzing and quantifying information security and cybersecurity risks.
This article examines factor analysis and its role in business, explores its definitions, various types, and provides real-world examples to illustrate its applications and benefits. With a clear understanding of what factor analysis is and how it works, you’ll be well-equipped to leverage this essential data analysis tool in making connections in your data for strategic decision-making.
Table of Contents
The Importance of Factor Analysis
In data science , factor analysis enables the identification of extra-dimensionality and hidden patterns in data and can be used to simplify data to select relevant variables for analysis.
Finding Hidden Patterns and Identifying Extra-Dimensionality
A primary purpose of factor analysis is dataset dimensionality reduction. This is accomplished by identifying latent variables, known as factors, that explain the common variance in a set of observed variables.
In essence, it helps data professionals sift through a large amount of data and extract the key dimensions that underlie the complexity. Factor analysis also allows data professionals to uncover hidden patterns or relationships within data, revealing the underlying structure that might not be apparent when looking at individual variables in isolation.
Simplifying Data and Selecting Variables
Factor analysis simplifies data interpretation. Instead of dealing with a multitude of variables, researchers can work with a smaller set of factors that capture the essential information. This simplification aids in creating more concise models and facilitates clearer communication of research findings.
Data professionals working with large datasets must routinely select a subset of variables most relevant or representative of the phenomenon under analysis or investigation. Factor analysis helps in this process by identifying the key variables that contribute to the factors, which can be used for further analysis.
How Does Factor Analysis Work?
Factor analysis is based on the idea that the observed variables in a dataset can be represented as linear combinations of a smaller number of unobserved, underlying factors. These factors are not directly measurable but are inferred from the patterns of correlations or covariances among the observed variables. Factor analysis typically consists of several fundamental steps.
1. Data Collection
The first step in factor analysis involves collecting data on a set of variables. These variables should be related in some way, and it’s assumed that they are influenced by a smaller number of underlying factors.
2. Covariance/Correlation Matrix
The next step is to compute the correlation matrix (if working with standardized variables) or covariance matrix (if working with non-standardized variables). These matrices help quantify the relationships between all pairs of variables, providing a basis for subsequent factor analysis steps.
Covariance Matrix
A covariance matrix is a mathematical construct that plays a critical role in statistics and multivariate analysis, particularly in the fields of linear algebra and probability theory. It provides a concise representation of the relationships between pairs of variables within a dataset.
Specifically, a covariance matrix is a square matrix in which each entry represents the covariance between two corresponding variables. Covariance measures how two variables change together; a positive covariance indicates that they tend to increase or decrease together, while a negative covariance suggests they move in opposite directions.
A covariance matrix is symmetric, meaning that the covariance between variable X and variable Y is the same as the covariance between Y and X. Additionally, the diagonal entries of the matrix represent the variances of individual variables, as the covariance of a variable with itself is its variance.
Correlation Matrix
A correlation matrix is a statistical tool used to quantify and represent the relationships between pairs of variables in a dataset. Unlike the covariance matrix, which measures the co-variability of variables, a correlation matrix standardizes this measure to a range between -1 and 1, providing a dimensionless value that indicates the strength and direction of the linear relationship between variables.
A correlation of 1 indicates a perfect positive linear relationship, while -1 signifies a perfect negative linear relationship. A correlation of 0 suggests no linear relationship. The diagonal of the correlation matrix always contains ones because each variable is perfectly correlated with itself.
Correlation matrices are particularly valuable for identifying and understanding the degree of association between variables, helping to reveal patterns and dependencies that might not be immediately apparent in raw data.
3. Factor Extraction
Factor extraction involves identifying the underlying factors that explain the common variance in the dataset. Various methods are used for factor extraction, including principal component analysis (PCA) and maximum likelihood estimation (MLE). These methods seek to identify the linear combinations of variables that capture the most variance in the data.
PCA is a dimensionality reduction and data transformation technique used in statistics, machine learning , and data analysis . Its primary goal is to simplify complex, high-dimensional data while preserving as much relevant information as possible.
PCA accomplishes this by identifying and extracting a set of orthogonal axes, known as principal components, that capture the maximum variance in the data. These principal components are linear combinations of the original variables and are ordered in terms of the amount of variance they explain, with the first component explaining the most variance, the second component explaining the second most, and so on. By projecting the data onto these principal components, you can reduce the dimensionality of the data while minimizing information loss.
As a powerful way to condense and simplify data, PCA is an invaluable tool for improving data interpretation and modeling efficiency, and is widely used for various purposes, including data visualization, noise reduction, and feature selection. It is particularly valuable in exploratory data analysis, where it helps researchers uncover underlying patterns and structures in high-dimensional datasets. In addition to dimensionality reduction, PCA can also aid in removing multicollinearity among variables, which is beneficial in regression analysis.
MLE is a fundamental statistical method used to estimate the parameters of a statistical model. The core premise behind MLE is to find the parameter values that maximize the likelihood function, which measures how well the model explains the observed data. In other words, MLE seeks to identify the parameter values that make the observed data the most probable under the assumed statistical model.
To perform MLE, one typically starts with a probability distribution or statistical model that relates the parameters to the observed data. The likelihood function is then constructed based on this model, and it quantifies the probability of observing the given data for different parameter values. MLE involves finding the values of the parameters that maximize this likelihood function.
In practice, this is often achieved through numerical optimization techniques, such as gradient descent or the Newton-Raphson method . MLE is highly regarded for its desirable properties, such as asymptotic efficiency and consistency, making it a widely used and respected method for parameter estimation in statistical modeling and data analysis.
4. Factor Rotation
Once factors are extracted, they are often rotated to achieve a simpler, more interpretable factor structure. Rotation methods like Varimax and Promax aim to make the factors more orthogonal or uncorrelated, which enhances their interpretability.


5. Factor Loadings
Factor loadings represent the strength and direction of the relationship between each variable and the underlying factors. These loadings indicate how much each variable contributes to a given factor and are used to interpret and label the factors.
6. Interpretation
The final step of factor analysis involves interpreting the factors and assigning meaning to them. Data professionals examine the factor loadings and consider the variables that are most strongly associated with each factor. This interpretation is a critical aspect of factor analysis, as it helps in understanding the latent structure of the data.
Types of Factor Analysis
Factor analysis comes in several variations, depending on the assumptions and constraints applied to the analysis. The two primary types are exploratory factor analysis (EFA) and confirmatory factor analysis (CFA).
Exploratory Factor Analysis (EFA)
EFA is used to explore and uncover the underlying structure of data. It is an open-ended approach that does not impose any specific structure on the factors. Instead, it allows the factors to emerge from the data. EFA is often used in the early stages of research when there is little prior knowledge about the relationships between variables.

Confirmatory Factor Analysis (CFA)
CFA, on the other hand, is a more hypothesis-driven approach—it starts with a predefined factor structure. The data is then tested to see if it fits that structure. This type of analysis is used when there is a theoretical model or prior knowledge about the expected relationships between variables and factors.
Benefits of Factor Analysis
Factor analysis offers several advantages to data professionals working a wide range of business/enterprise settings:
- Data reduction and enhanced interpretability. By reducing the dimensionality of data, you can more easily analyze and interpret complex datasets. This results in enhanced data interpretation and explainability—by identifying latent factors, factor analysis provides a more meaningful interpretation of the relationships among variables, making it easier to understand complex phenomena.
- Multivariable selection and analysis. Factor analysis aids in variable selection by identifying the most important variables that contribute to the factors. This is especially valuable when working with large datasets. Crucially, factor analysis is a form of multivariate analysis, which is essential in use cases that require examining relationships between multiple variables simultaneously.
Factor Analysis Examples
Organizations can use factor analysis in a wide range of applications to identify underlying factors or latent variables that explain patterns in data.
Market Research
Market researchers often use factor analysis to identify the key factors that influence consumer preferences. For example, a survey may collect data on various product attributes like price, brand reputation, quality, and customer service. Factor analysis can help determine which factors have the most significant impact on consumers’ product choices. By identifying underlying factors, businesses can tailor their product development and marketing strategies to meet consumer needs more effectively.
Financial Risk Analysis
Factor analysis is commonly used in finance to analyze and manage financial risk. By examining various economic indicators, asset returns, and market conditions, factor analysis helps investors and portfolio managers understand how different factors contribute to the overall risk and return of an investment portfolio.
Customer Segmentation
Businesses often use factor analysis to identify customer segments based on their purchasing behavior, preferences, and demographic information. By analyzing these factors, companies can create better targeted marketing strategies and product offerings.
Employee Engagement
Factor analysis can be used to identify the underlying factors that contribute to employee engagement and job satisfaction. This information helps businesses improve workplace conditions and increase employee retention.
Brand Perception
Companies may employ factor analysis to understand how customers perceive their brand. By analyzing factors like brand image, trust, and quality, businesses can make informed decisions to strengthen their brand and reputation.
Product Quality Controls
In manufacturing, factor analysis can help identify the key factors affecting product quality. This analysis can lead to process improvements and quality control measures, ultimately reducing defects and enhancing customer satisfaction.
These examples are just a handful of use cases that demonstrate how factor analysis can be applied in business. As a versatile statistical tool, it can be adapted to various data-driven decision-making processes for helping organizations gain deeper insights and make informed choices.
Factor Analysis vs. FAIR
Factor analysis is different from Fact Analysis of Information Risk, or FAIR. Factor analysis encompasses statistical methods for data reduction and identifying underlying patterns in various fields, while FAIR is a specific framework and methodology used for analyzing and quantifying information security and cybersecurity risks. Unlike traditional factor analysis, which deals strictly with data patterns, FAIR focuses specifically on information and cyber risk factors to help organizations prioritize and manage their cybersecurity efforts effectively.
Bottom Line
With factor analysis in their cachet of tools, data professionals and business researchers have a powerful and battle-tested statistical technique for simplifying data, identifying latent structures, and understanding complex relationships among variables. Through these discoveries, organizations can better explain observed relationships among a set of variables by reducing complex data into a more manageable form, making it easier to understand, interpret, and draw meaningful conclusions.
Read Top 7 Data Analytics Tools to learn about the best enterprise software to help analyze and visualize data.
Subscribe to Data Insider
Learn the latest news and best practices about data science, big data analytics, artificial intelligence, data security, and more.
Similar articles
8 best data analytics tools: gain data-driven advantage in 2024, common data visualization examples: transform numbers into narratives, what is data management a guide to systems, processes, and tools, get the free newsletter.
Subscribe to Data Insider for top news, trends & analysis
Latest Articles
Exploring multi-tenant architecture: a..., 8 best data analytics..., common data visualization examples:..., what is data management....

Factor Analysis: From Novice to Expert in Simple Steps
Key takeaways
- Factor analysis is a statistical method used to identify underlying factors that explain the variation in observed variables.
- Factor analysis can help researchers reduce the number of variables in a dataset and identify the most important variables that contribute to the variation in the data.
- Understanding factor analysis is essential for researchers who want to analyze data and identify patterns in large datasets.
Factor Analysis is a powerful statistical technique that can help you identify the underlying factors in your data and gain deeper insights into the relationships between variables
It is a popular technique used in various fields, including psychology, marketing, and finance.
Whether you’re a data analyst, a business owner, or just someone who’s interested in data science, this post will give you a better understanding of how to use Factor Analysis to make more informed decisions.
Understanding Factor Analysis
Factor Analysis is a statistical method that is used to identify the underlying structure of a set of variables. It is commonly used in a wide range of fields, including psychology, sociology, and market research.
In this section, we will explore the basics of Factor Analysis and how it works.
What is Factor Analysis?
Factor Analysis is a statistical technique used to identify underlying factors in a set of data. It is a powerful tool for data analysis that can help you gain insights into the relationships between variables.
Factor Analysis works by reducing the number of variables in your data and identifying the underlying factors that explain the correlations between them.
There are two main types of Factor Analysis: Exploratory Factor Analysis (EFA) and Confirmatory Factor Analysis (CFA).
EFA is used to identify underlying factors in your data, while CFA is used to confirm a pre-existing factor structure. Factor Analysis requires a large sample size and a correlation matrix.
Why Use Factor Analysis?
By identifying the underlying factors in your data, you can reduce the number of variables and gain a deeper understanding of the relationships between them.
Factor Analysis is particularly useful in fields such as market research, psychology, and social sciences. It can help you identify the underlying factors that influence consumer behavior, employee satisfaction, and other important variables.
What is the difference between factor analysis and factorial analysis?
Factor analysis and factorial analysis are often confused, but they are different techniques.
Factor analysis is used to identify the underlying factors that affect a set of variables, whereas factorial analysis is used to test the effect of one or more independent variables on a dependent variable.
Factorial analysis is also known as ANOVA (Analysis of Variance).
Cluster Analysis vs Factor Analysis
Factor Analysis and Cluster Analysis are two commonly used statistical methods that are often confused with each other. While both methods are used to identify patterns in data, they are fundamentally different.
Cluster Analysis is used to group similar cases or observations together based on their characteristics.
On the other hand, Factor Analysis is used to identify underlying factors that explain the correlations between a set of observed variables.

Types of Factor Analysis
Factor analysis is a statistical method used to identify patterns in data and reduce the number of variables in a dataset. There are three primary types of factor analysis:
- Principal Component Analysis (PCA)
- Exploratory Factor Analysis (EFA)
- Confirmatory Factor Analysis (CFA).
1. Principal Component Analysis
PCA is a technique that is used to transform a large number of variables into a smaller number of uncorrelated variables known as principal components. The principal components are ordered by the amount of variance they explain in the original data.
The first principal component explains the most variance, the second principal component explains the second most variance, and so on. PCA is often used as a data reduction technique to simplify complex datasets.
2. Exploratory Factor Analysis
EFA is a technique used to identify underlying factors in a dataset. It is used when the researcher does not have a preconceived notion of the number of factors or what those factors might be.
EFA is an iterative process that involves extracting factors, examining the factor loadings, and refining the factor structure until a satisfactory solution is obtained. The factors extracted in EFA are not predetermined, and the researcher must use their judgment to interpret the factors.
3. Confirmatory Factor Analysis
CFA is a technique used to test a priori hypotheses about the factor structure of a dataset. It is used when the researcher has a preconceived notion of the number of factors and what those factors might be.
CFA involves specifying a model that reflects the hypothesized factor structure and testing that model against the data . The fit of the model is assessed using various fit indices, and modifications to the model may be made to improve the fit.
In summary,
- PCA is used to transform a large number of variables into a smaller number of uncorrelated variables
- EFA is used to identify underlying factors in a dataset
- CFA is used to test a priori hypotheses about the factor structure of a dataset.

Statistical Methods in Factor Analysis
Factor analysis is a statistical method used to examine the interrelationships among a large number of variables and identify underlying factors that explain the patterns of responses.
This method is widely used in various fields, including psychology, market research, sociology, and education.
Understanding Factor Scores
Factor analysis involves grouping a large number of variables into a smaller number of factors that are related to each other. These factors are then used to create factor scores, which are estimates of a person’s standing on each factor.
Factor scores are useful for a variety of purposes, such as predicting customer satisfaction or identifying personality traits.
Factor scores can be calculated using a variety of statistical methods, including principal components analysis (PCA), maximum likelihood estimation (MLE), and common factor analysis (CFA).
- PCA is a commonly used method that identifies the factors that account for the most variance in the data.
- MLE is a more complex method that estimates the parameters of the factor model using a likelihood function.
- CFA is a method that assumes that each variable is related to only one factor, while PCA and MLE allow for variables to be related to multiple factors.

The Mathematics Behind Factor Analysis
Factor analysis is based on the idea that a small number of unobserved variables, called factors, can explain the variation in a larger number of observed variables.
Assumptions in Factor Analysis
There are several assumptions that underlie factor analysis.
- First, it is assumed that the observed variables are correlated with each other . This correlation can be positive or negative, and it indicates that the variables are related in some way.
- Second, it is assumed that there are a small number of underlying factors that are responsible for the observed correlations between the variables . These factors are unobserved variables that explain the variation in the observed variables.
- Third, it is assumed that the factors are uncorrelated with each other . This is known as the assumption of orthogonal rotation. Orthogonal rotation means that the factors are independent of each other, and they do not overlap. This assumption simplifies the interpretation of the results, as it allows each factor to be interpreted as a distinct construct.
- Fourth, it is assumed that the factors are measured without error . This means that the factors are perfectly measured, and there is no measurement error associated with them. In practice, this assumption is rarely met, as there is always some degree of measurement error associated with any measurement.
Tips : If you are curios to learn more about data & analytcs and related topics, then check out all of our posts related to data analytics
Orthogonal Rotation
Orthogonal rotation is a technique used in factor analysis to simplify the interpretation of the results . It involves rotating the factors so that they are uncorrelated with each other. This makes it easier to interpret the results, as each factor can be interpreted as a distinct construct.
There are several methods of orthogonal rotation, including varimax, quartimax, and equimax.
- The varimax method is the most commonly used method, as it maximizes the variance of the factor loadings
- The quartimax method, on the other hand, minimizes the number of factors that are required to explain the correlations between the variables.
Tools for Factor Analysis
There are several statistical software packages that can be used for factor analysis. In this section, we will discuss some of the most popular ones.
Factor Analysis Using SPSS
SPSS (Statistical Package for the Social Sciences) is one of the most widely used statistical software packages for factor analysis. It provides a user-friendly interface that makes it easy to perform exploratory and confirmatory factor analysis.
SPSS also offers a variety of options for extracting factors, including principal components analysis, maximum likelihood, and principal axis factoring.
To perform factor analysis in SPSS , you first need to import your data into the software. Once your data is loaded, you can select the variables you want to include in your analysis and specify the extraction method and rotation method.
SPSS also provides several options for assessing the goodness of fit of your factor model, including the Kaiser-Meyer-Olkin measure and Bartlett’s test of sphericity.
Factor Analysis in R
R is a popular open-source programming language and software environment for statistical computing and graphics. It provides a wide range of packages for performing factor analysis, including the psych, lavaan, and FactoMineR packages.
To perform factor analysis in R , you first need to import your data into the software. Once your data is loaded, you can use the functions provided by the factor analysis package of your choice to extract factors and estimate factor loadings.
R also provides several options for assessing the goodness of fit of your factor model, including the chi-squared test and the root mean square error of approximation.
Stata Factor Analysis
Stata is a popular statistical software package that is widely used in social science research. It provides a user-friendly interface for performing exploratory and confirmatory factor analysis.
Stata also offers a variety of options for extracting factors, including principal components analysis, maximum likelihood, and principal axis factoring.
To perform factor analysis in Stata , you first need to import your data into the software.
Once your data is loaded, you can select the variables you want to include in your analysis and specify the extraction method and rotation method.
Stata also provides several options for assessing the goodness of fit of your factor model, including the Kaiser-Meyer-Olkin measure and Bartlett’s test of sphericity.
Factor Analysis in Different Areas
Factor analysis is a statistical method that is widely used in different fields. It helps in identifying the underlying structure of a large set of variables. Here are some examples of how factor analysis is used in different areas:
Factor Analysis in Psychology
Factor analysis is commonly used in psychology to identify the underlying factors that contribute to a particular trait or behavior.
For example, researchers may use factor analysis to identify the underlying factors that contribute to depression or anxiety.
By identifying these factors, psychologists can develop more effective treatments for these disorders.
Factor Analysis in Health and Education
Factor analysis is also used in health and education to identify the underlying factors that contribute to certain outcomes.
For example, researchers may use factor analysis to identify the underlying factors that contribute to academic achievement or health outcomes . By identifying these factors, educators and health professionals can develop more effective interventions to improve outcomes.
Factor Analysis in Social Sciences
Factor analysis is widely used in social sciences such as sociology, anthropology, and political science. It helps in identifying the underlying factors that contribute to a particular social phenomenon.
For example, researchers may use factor analysis to identify the underlying factors that contribute to political attitudes or social inequality.
Factor Analysis in Biology
Factor analysis is also useful in biology to identify underlying factors that influence different biological phenomena, such as growth, reproduction, and adaptation.
By identifying these underlying factors, biologists can better understand the complex nature of biological systems and develop more effective interventions.

In conclusion, factor analysis is a powerful statistical method that is widely used in different fields. It helps in identifying the underlying factors that contribute to a particular outcome, which is useful in developing more effective interventions and theoretical models.
Factor Analysis in Machine Learning
Factor analysis is a powerful technique used in machine learning to simplify complex datasets by identifying underlying factors and their interconnections.
In essence, it is a method for reducing the number of variables in a dataset while retaining as much of the original information as possible.
One of the key benefits of factor analysis is that it can help to identify and address multicollinearity, which occurs when two or more variables are highly correlated with each other.
By identifying the underlying factors that contribute to this correlation, factor analysis can help to reduce the number of variables in a dataset and improve the accuracy of machine learning models .
Practical Considerations in Factor Analysis
When conducting a factor analysis, there are several practical considerations that you should keep in mind to ensure that your results are accurate and meaningful.
1. Sample Size
One of the most important considerations is the size of your sample. Generally, a larger sample size is better because it increases the accuracy of your results.
However, there is no hard and fast rule about what constitutes a “large enough” sample size. As a general rule, you should aim for a sample size of at least 100, but you may need more depending on the complexity of your analysis.
2. Uniqueness
Another important consideration is the uniqueness of your variables. Uniqueness refers to the degree to which each variable is distinct from all the other variables in your analysis.
If your variables are highly unique, it may be more difficult to identify meaningful factors. On the other hand, if your variables are highly correlated, it may be difficult to separate them into distinct factors.
3. Iterations
Factor analysis is an iterative process, which means that you may need to run multiple iterations to arrive at a stable solution.
Each iteration will refine the factor structure until it converges on a stable solution. It’s important to be patient and not rush the process, as running too few iterations can lead to inaccurate results.
4. Component Score
Once you have identified your factors, you may want to compute component scores for each observation in your dataset.
Component scores are a way of summarizing the information contained in your variables into a single score for each observation. These scores can be useful for subsequent analyses, such as regression or discriminant analysis.
5. Characteristic Roots
Finally, it’s important to pay attention to the characteristic roots of your factors. The characteristic roots represent the amount of variance explained by each factor.
Generally, you should aim to retain factors with characteristic roots greater than one, as these factors explain more variance than a single variable. However, you should also consider the interpretability of your factors when deciding how many to retain.
Overall, factor analysis is a powerful tool for exploring the underlying structure of your data. By keeping these practical considerations in mind, you can ensure that your results are accurate and meaningful.

Advanced Concepts in Factor Analysis
Now that you have a basic understanding of factor analysis, it’s time to dive into some of the more advanced concepts.
Common Factor Analysis
Common factor analysis is a type of factor analysis that assumes that there are underlying factors that are common to all of the observed variables.
This is in contrast to principal component analysis, which assumes that each observed variable is a linear combination of the underlying factors. Common factor analysis is useful when you want to identify the underlying factors that are common to a set of variables.
Principal Axis Factoring
Principal axis factoring is a method of factor extraction that is similar to principal component analysis, but with a few key differences.
Unlike principal component analysis, principal axis factoring allows for the possibility of negative factor loadings. It also uses a different method of determining the number of factors to extract, known as the scree test.
Maximum Likelihood
Maximum likelihood is a method of estimating the parameters of a statistical model. In the context of factor analysis, maximum likelihood estimation is used to estimate the factor loadings, factor variances, and error variances.
Maximum likelihood estimation is often preferred over other methods because it is efficient and provides unbiased estimates.
Factor Scores
Factor scores are estimates of the underlying factors for each individual in a sample. They are calculated by multiplying the individual’s scores on the observed variables by the factor loadings and summing across the factors.
Factor scores are useful for a variety of purposes, including predicting outcomes and identifying subgroups of individuals with similar factor profiles.
Communality
Communality is a measure of the proportion of variance in an observed variable that is accounted for by the underlying factors.
It ranges from 0 to 1 and can be interpreted as the amount of “shared variance” between the observed variable and the factors. Higher communality values indicate that the observed variable is more strongly related to the underlying factors.
Factor Extraction
Factor extraction is the process of identifying the underlying factors in a set of observed variables. There are many different methods of factor extraction, including principal component analysis, common factor analysis, and principal axis factoring. The choice of method depends on the research question and the characteristics of the data.

Factor Data Analysis: The Essentials
Factor Analysis is a powerful statistical technique that can help you find underlying factors in your data. By identifying these factors, you can gain insights into the relationships between variables and make more informed decisions.
Factor Analysis is a versatile technique that can be used in a variety of fields, including market research, psychology, and social sciences.
With its ability to reduce the number of variables and find underlying factors, Factor Analysis is an essential tool for any data analyst.
Key Takeaways: Data Structuring with Factor Analysis
- Factor Analysis is a statistical technique used to identify underlying factors in your data.
- Factor Analysis can be used in combination with other statistical techniques, such as regression analysis, to gain deeper insights into your data.
- It can reduce the number of variables and help you gain insights into the relationships between variables.
- Factor Analysis can be used in a variety of fields, including market research, psychology, and social sciences.
- There are two main types of Factor Analysis: Exploratory Factor Analysis (EFA) and Confirmatory Factor Analysis (CFA). EFA is used to identify underlying factors in your data, while CFA is used to confirm a pre-existing factor structure.
- Factor Analysis requires a large sample size and a correlation matrix.
FAQ: Factor Analytics
When should factor analysis be used.
Factor analysis is a statistical method that is used to identify the underlying structure of a set of variables. It is often used in social science research to identify the latent variables that may be driving the observed correlations between variables. Factor analysis can be used when you have a large number of variables and you want to reduce them to a smaller number of factors. It is also useful when you want to identify the underlying structure of a set of variables, or when you want to test hypotheses about the relationships between variables.
What are the assumptions of factor analysis?
Factor analysis assumes that the variables are normally distributed, that there is no multicollinearity among the variables, and that the sample size is adequate. It also assumes that the factors are uncorrelated with each other, and that the factors are orthogonal.
What are the steps of factor analysis?
The steps of factor analysis include selecting the variables to be analyzed, deciding on the number of factors to be extracted, determining the initial factor solution, rotating the factor solution to make it more interpretable, and interpreting the factor solution.
What is confirmatory factor analysis?
Confirmatory factor analysis is a statistical method that is used to confirm or test a hypothesized factor structure. It is used when you have a theoretical model of the underlying structure of a set of variables and you want to test whether the data fit the model. Confirmatory factor analysis is often used in social science research to test theories about the relationships between variables.
What is the best use case for factor analysis?
Factor analysis is useful when you have a large number of variables and you want to reduce them to a smaller number of factors. It is also useful when you want to identify the underlying structure of a set of variables, or when you want to test hypotheses about the relationships between variables. Factor analysis can be used in a wide range of fields, including psychology, sociology, education, and business.
How do you interpret factor analysis results?
The interpretation of factor analysis results involves examining the factor loadings, which are the correlations between the variables and the factors. A high factor loading indicates that the variable is strongly related to the factor, while a low factor loading indicates that the variable is not strongly related to the factor. The interpretation of factor analysis results also involves examining the eigenvalues, which indicate the amount of variance explained by each factor, and the scree plot, which can help determine the number of factors to retain.
Meet Eric, the data "guru" behind Datarundown. When he's not crunching numbers, you can find him running marathons, playing video games, and trying to win the Fantasy Premier League using his predictions model (not going so well).
Eric passionate about helping businesses make sense of their data and turning it into actionable insights. Follow along on Datarundown for all the latest insights and analysis from the data world.
Related Posts

Data Mining Tools for Cluster Analysis: A Comprehensive Guide
- Clustering Data Mining

6 Different Types of Clustering: All You Need To Know!

5 Use Cases and Practical Examples of Hierarchical Clustering

Factor Analysis 101: The Basics
- Market Research , Survey Tips
What is Factor Analysis?
Factor analysis is a powerful data reduction technique that enables researchers to investigate concepts that cannot easily be measured directly. By boiling down a large number of variables into a handful of comprehensible underlying factors, factor analysis results in easy-to-understand, actionable data.
By applying this method to your research, you can spot trends faster and see themes throughout your datasets, enabling you to learn what the data points have in common.
Unlike statistical methods such as regression analysis , factor analysis does not require defined variables.
Factor analysis is most commonly used to identify the relationship between all of the variables included in a given dataset.
The Objectives of Factor Analysis
Think of factor analysis as shrink wrap. When applied to a large amount of data, it compresses the set into a smaller set that is far more manageable, and easier to understand.
The overall objective of factor analysis can be broken down into four smaller objectives:
- To definitively understand how many factors are needed to explain common themes amongst a given set of variables.
- To determine the extent to which each variable in the dataset is associated with a common theme or factor.
- To provide an interpretation of the common factors in the dataset.
- To determine the degree to which each observed data point represents each theme or factor.
When to Use Factor Analysis
Determining when to use particular statistical methods to get the most insight out of your data can be tricky.
When considering factor analysis, have your goal top-of-mind.
There are three main forms of factor analysis. If your goal aligns to any of these forms, then you should choose factor analysis as your statistical method of choice:
Exploratory Factor Analysi s should be used when you need to develop a hypothesis about a relationship between variables.
Confirmatory Factor Analysis should be used to test a hypothesis about the relationship between variables.
Construct Validity should be used to test the degree to which your survey actually measures what it is intended to measure.
How To Ensure Your Survey is Optimized for Factor Analysis
If you know that you’ll want to perform a factor analysis on response data from a survey, there are a few things you can do ahead of time to ensure that your analysis will be straightforward, informative, and actionable.
Identify and Target Enough Respondents
Large datasets are the lifeblood of factor analysis. You’ll need large groups of survey respondents, often found through panel services , for factor analysis to yield significant results.
While variables such as population size and your topic of interest will influence how many respondents you need, it’s best to maintain a “more respondents the better” mindset.
The More Questions, The Better
While designing your survey , load in as many specific questions as possible. Factor analysis will fall flat if your survey only has a few broad questions.
The ultimate goal of factor analysis is to take a broad concept and simplify it by considering more granular, contextual information, so this approach will provide you the results you’re looking for.
Aim for Quantitative Data
If you’re looking to perform a factor analysis, you’ll want to avoid having open-ended survey questions .
By providing answer options in the form of scales (whether they be Likert Scales , numerical scales, or even ‘yes/no’ scales) you’ll save yourself a world of trouble when you begin conducting your factor analysis. Just make sure that you’re using the same scaled answer options as often as possible.
See all blog posts >

- Alchemer Survey , Survey Tips

- Alchemer Pulse , Customer Experience

- Customer Experience , Customer Feedback , Voice of the Customer
See it in Action
- Privacy Overview
- Strictly Necessary Cookies
- 3rd Party Cookies
This website uses cookies so that we can provide you with the best user experience possible. Cookie information is stored in your browser and performs functions such as recognising you when you return to our website and helping our team to understand which sections of the website you find most interesting and useful.
Strictly Necessary Cookie should be enabled at all times so that we can save your preferences for cookie settings.
If you disable this cookie, we will not be able to save your preferences. This means that every time you visit this website you will need to enable or disable cookies again.
This website uses Google Analytics to collect anonymous information such as the number of visitors to the site, and the most popular pages.
Keeping this cookie enabled helps us to improve our website.
Please enable Strictly Necessary Cookies first so that we can save your preferences!
Factor Analysis in Marketing Research
- Home > What We Do > Research Methods > Statistical Techniques > Factor Analysis in Marketing Research
Factor analysis in marketing research aims to describe a large number of variables or questions by using a reduced set of underlying variables, called factors.
Contact Us >
To find out more about factor analysis and how it can help your business
What is factor analysis in marketing research?
Factor analysis explains a pattern of similarity between observed variables. Questions which belong to one factor are highly correlated with each other; unlike cluster analysis, which classifies respondents, factor analysis groups variables.
There are two types of factor analysis in marketing research: exploratory and confirmatory. Exploratory factor analysis is driven by the data, i.e. the data determines the factors. Confirmatory factor analysis, used in structural equation modelling, tests and confirms hypotheses.
Factor analysis in market research is often used in customer satisfaction studies to identify underlying service dimensions, and in profiling studies to determine core attitudes. For example, as part of a national survey on political opinions, respondents may answer three separate questions regarding environmental policy, reflecting issues at the local, regional and national level. Factor analysis can be used to establish whether the three measures do, in fact, measure the same thing.
It can also prove to be useful when a lengthy questionnaire needs to be shortened, but still retain key questions. Factor analysis indicates which questions can be omitted without losing too much information.
Contact Us >
Privacy Overview
| Cookie | Duration | Description |
|---|---|---|
| __hssrc | session | This cookie is set by Hubspot whenever it changes the session cookie. The __hssrc cookie set to 1 indicates that the user has restarted the browser, and if the cookie does not exist, it is assumed to be a new session. |
| cookielawinfo-checkbox-advertisement | 1 year | Set by the GDPR Cookie Consent plugin, this cookie is used to record the user consent for the cookies in the "Advertisement" category . |
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| CookieLawInfoConsent | 1 year | Records the default button state of the corresponding category & the status of CCPA. It works only in coordination with the primary cookie. |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |
| Cookie | Duration | Description |
|---|---|---|
| __cf_bm | 30 minutes | This cookie, set by Cloudflare, is used to support Cloudflare Bot Management. |
| __hssc | 30 minutes | HubSpot sets this cookie to keep track of sessions and to determine if HubSpot should increment the session number and timestamps in the __hstc cookie. |
| bcookie | 2 years | LinkedIn sets this cookie from LinkedIn share buttons and ad tags to recognize browser ID. |
| bscookie | 2 years | LinkedIn sets this cookie to store performed actions on the website. |
| lang | session | LinkedIn sets this cookie to remember a user's language setting. |
| lidc | 1 day | LinkedIn sets the lidc cookie to facilitate data center selection. |
| UserMatchHistory | 1 month | LinkedIn sets this cookie for LinkedIn Ads ID syncing. |
| Cookie | Duration | Description |
|---|---|---|
| __hstc | 5 months 27 days | This is the main cookie set by Hubspot, for tracking visitors. It contains the domain, initial timestamp (first visit), last timestamp (last visit), current timestamp (this visit), and session number (increments for each subsequent session). |
| _ga | 2 years | The _ga cookie, installed by Google Analytics, calculates visitor, session and campaign data and also keeps track of site usage for the site's analytics report. The cookie stores information anonymously and assigns a randomly generated number to recognize unique visitors. |
| _gat_gtag_UA_3031018_3 | 1 minute | Set by Google to distinguish users. |
| _gid | 1 day | Installed by Google Analytics, _gid cookie stores information on how visitors use a website, while also creating an analytics report of the website's performance. Some of the data that are collected include the number of visitors, their source, and the pages they visit anonymously. |
| CONSENT | 2 years | YouTube sets this cookie via embedded youtube-videos and registers anonymous statistical data. |
| hubspotutk | 5 months 27 days | HubSpot sets this cookie to keep track of the visitors to the website. This cookie is passed to HubSpot on form submission and used when deduplicating contacts. |
| undefined | never | Wistia sets this cookie to collect data on visitor interaction with the website's video-content, to make the website's video-content more relevant for the visitor. |
| vuid | 2 years | Vimeo installs this cookie to collect tracking information by setting a unique ID to embed videos to the website. |
| Cookie | Duration | Description |
|---|---|---|
| VISITOR_INFO1_LIVE | 5 months 27 days | A cookie set by YouTube to measure bandwidth that determines whether the user gets the new or old player interface. |
| YSC | session | YSC cookie is set by Youtube and is used to track the views of embedded videos on Youtube pages. |
| yt-remote-connected-devices | never | YouTube sets this cookie to store the video preferences of the user using embedded YouTube video. |
| yt-remote-device-id | never | YouTube sets this cookie to store the video preferences of the user using embedded YouTube video. |
| Cookie | Duration | Description |
|---|---|---|
| AnalyticsSyncHistory | 1 month | No description |
| closest_office_location | 1 month | No description |
| li_gc | 2 years | No description |
| loglevel | never | No description available. |
| ssi--lastInteraction | 10 minutes | This cookie is used for storing the date of last secure session the visitor had when visiting the site. |
| ssi--sessionId | 1 year | This cookie is used for storing the session ID which helps in reusing the one the visitor had already used. |
| user_country | 1 month | No description available. |

IMAGES
VIDEO
COMMENTS
Factor analysis is a statistical technique that is used to identify the underlying structure of a relatively large set of variables and to explain these variables in terms of a smaller number of common underlying factors. It helps to investigate the latent relationships between observed variables.
Researchers frequently use factor analysis in psychology, sociology, marketing, and machine learning. Let’s dig deeper into the goals of factor analysis, critical methodology choices, and an example. This guide provides practical advice for performing factor analysis.
Factor Analysis is a statistical technique to reduce dimensions of a given dataset and procure super-variables out of the vast number of observed variables.
Factor analysis is a commonly used data reduction statistical technique within the context of market research. The goal of factor analysis is to discover relationships between variables within a dataset by looking at correlations.
Factor analysis is the practice of condensing many variables into just a few, so that your research data is easier to work with.
Factor analysis is a powerful statistical technique used by data professionals in various business domains to uncover underlying data structures or latent variables.
Factor analysis is a sophisticated statistical method aimed at reducing a large number of variables into a smaller set of factors. This technique is valuable for extracting the maximum common variance from all variables, transforming them into a single score for further analysis.
Factor analysis is a statistical method used to identify underlying factors that explain the variation in observed variables. Factor analysis can help researchers reduce the number of variables in a dataset and identify the most important variables that contribute to the variation in the data.
Conducting a factor analysis allows you to make sense of a dataset by uncovering latent trends to determine exactly what the data points in a set have in common. Learn the objectives of factor analysis, when to use it, and how to optimize your surveys.
What is factor analysis in marketing research? Factor analysis explains a pattern of similarity between observed variables. Questions which belong to one factor are highly correlated with each other; unlike cluster analysis, which classifies respondents, factor analysis groups variables.